2024年高职单招《数学(中职)》每日一练试题11月22日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、不等式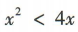 的解集为()
的解集为()
答 案:A
解 析:不等式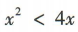 可化为
可化为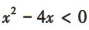 ,
,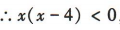 ,解得
,解得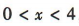 ,即不等式
,即不等式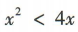 的解集为
的解集为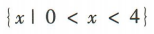 .
.
2、当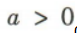 ,且m,n∈R时,下列选项不正确的是()
,且m,n∈R时,下列选项不正确的是()
答 案:A
解 析:
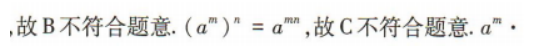
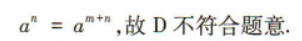
3、设点P为直线x+y-4=0上的动点,点A(-2,0),B(2,0),则|PA|+|PB|的最小值为()
答 案:A
解 析:设点 C(x,y)为点B(2,0)关于直线x+y-4=0的对称点,则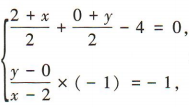 解得
解得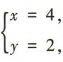 所以C(4,2),所以
所以C(4,2),所以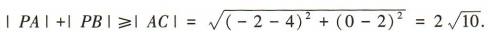
4、若直线x-y+1=0与圆(x-a)²+y²=2有公共点,则实数a的取值范围是()
- A:[-3,-1]
- B:(-3,1)
- C:[-3,1]
- D:(-∞,-3)U(-1,+∞)
答 案:C
解 析:由方程(x-a)²+y²=2得圆的圆心坐标为(a,0),半径为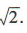 因为直线x-y+1=0与圆有公共点,所以
因为直线x-y+1=0与圆有公共点,所以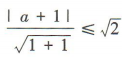 ,即|a+1|≤2,解得-3≤a≤1.
,即|a+1|≤2,解得-3≤a≤1.
填空题
1、函数f(x)=3-2cos4x的最大值为()
答 案:5
解 析: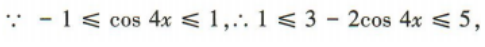 所以最大值是5
所以最大值是5
2、不等式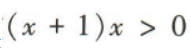 的解集是()
的解集是()
答 案:(-∞,-1)∪(0,+∞)
解 析: 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)
3、如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=2,则二面角A-DD1-B的正切值为()

答 案: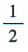
解 析:易得 ,
, 平面角.在
平面角.在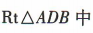 ,AB=1AD=2,
,AB=1AD=2,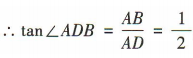 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为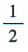 .
.
4、已知函数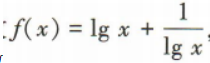 则f(100)=()
则f(100)=()
答 案: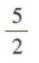
解 析: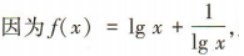
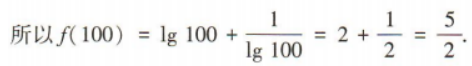
简答题
1、已知△ABC的内角A,B,C的对边分别为a,b,c,且a+b=11,c=7, (1)求a的值;
(2)求sinA和△ABC的面积.
(1)求a的值;
(2)求sinA和△ABC的面积.
答 案:




2、已知函数f(x)=x2+2ax+2,x∈[-5,5].
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)若f(x)在区间[-5,5]上是单调函数,求实数a的取值范围
答 案:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1, 所以在区间[-5,5]上,当x=1时,函数f(x)取得最小值,为f(1)=1,
当x=-5时,函数f(x)取得最大值,为f(-5)=37
(2)f(x)=x2+2ax+2=(x+a)2+2-a2.
若f(x)在区间[-5,5]上是单调函数,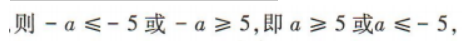 故实数a的取值范围为(-∞,-5]∪[5,+∞).
故实数a的取值范围为(-∞,-5]∪[5,+∞).
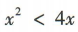 的解集为()
的解集为()
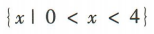
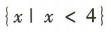
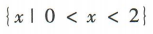
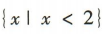
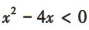 ,
,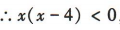 ,解得
,解得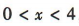 ,即不等式
,即不等式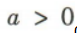 ,且m,n∈R时,下列选项不正确的是()
,且m,n∈R时,下列选项不正确的是()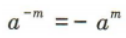

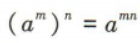
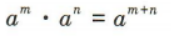

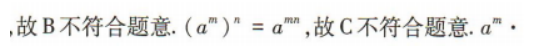
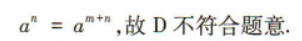

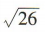
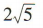
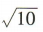
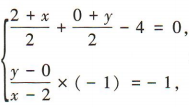 解得
解得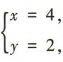 所以C(4,2),所以
所以C(4,2),所以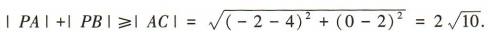
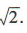 因为直线x-y+1=0与圆有公共点,所以
因为直线x-y+1=0与圆有公共点,所以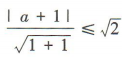 ,即|a+1|≤2,解得-3≤a≤1.
,即|a+1|≤2,解得-3≤a≤1.
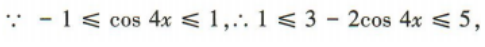 所以最大值是5
所以最大值是5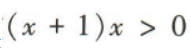 的解集是()
的解集是() 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)

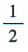
 ,
, 平面角.在
平面角.在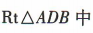 ,AB=1AD=2,
,AB=1AD=2,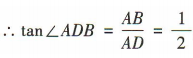 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为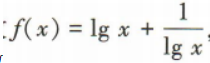 则f(100)=()
则f(100)=()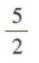
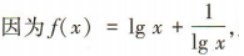
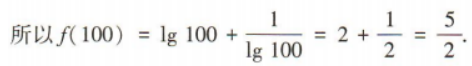
 (1)求a的值;
(2)求sinA和△ABC的面积.
(1)求a的值;
(2)求sinA和△ABC的面积.




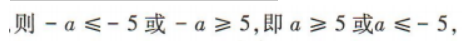 故实数a的取值范围为(-∞,-5]∪[5,+∞).
故实数a的取值范围为(-∞,-5]∪[5,+∞).


