2024年高职单招《数学(中职)》每日一练试题11月18日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知函数f(x)=tanx,则下列说法正确的是()
- A:f(x)在整个定义域上为增函数
- B:f(x)在整个定义域上为减函数
- C:
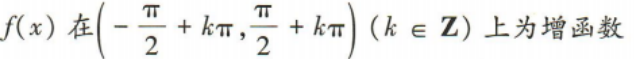
- D:
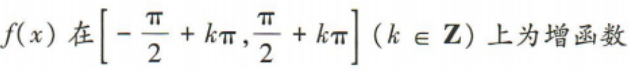
答 案:C
解 析:
 上为增函数,但在整个定义域上不是单调函数.
上为增函数,但在整个定义域上不是单调函数.
2、△ABC中,
答 案:A
解 析:

3、315°=()
答 案:C
解 析:
4、当 时,函数y=ax与函数y=(a-1)x²+x在同一坐标系内的图象可能是()
时,函数y=ax与函数y=(a-1)x²+x在同一坐标系内的图象可能是()
答 案:D
解 析:由 得指数函数y=ax是增函数,排除A,B选项;由
得指数函数y=ax是增函数,排除A,B选项;由 得二次函数y=(a-1)x²+x的图象开口向上,对称轴为直线
得二次函数y=(a-1)x²+x的图象开口向上,对称轴为直线 ,位于y轴左侧,排除C选项.故选D.
,位于y轴左侧,排除C选项.故选D.
填空题
1、不等式 的解集为()(用区间表示)
的解集为()(用区间表示)
答 案:(-1,0)∪(0,+∞)
解 析: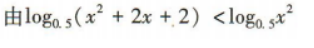
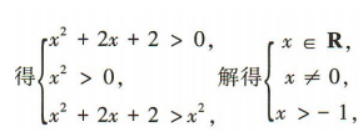

2、在二项式(x-1)6的展开式中,系数最小的项是第()项.
答 案:4
解 析:易知(x-1)6的展开式的通项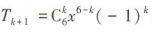 ,所以当k取1,3,5时,系数小于0.由组合数的性质知当日仅当k=3时,
,所以当k取1,3,5时,系数小于0.由组合数的性质知当日仅当k=3时,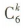 取最大值,所以当k=3时,系数取最小值,所以系数最小的项是第4项.
取最大值,所以当k=3时,系数取最小值,所以系数最小的项是第4项.
3、已知函数f(x)=2x2-4kx-5在区间[-1,2]上不具有单调性,则k的取值范围是()
答 案:(-1,2)
解 析:函数f(x)=2x2-4kx-5图像的对称轴为直线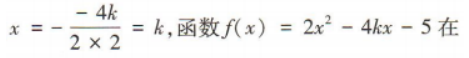

4、已知点P在圆x2+(y-1)2=9上,若点P到直线y=x+1的距离为3,则满足条件的点P的个数为()
答 案:2
解 析:易知圆x2+(y-1)2=9的圆心为(0,1),半径r=3.因为直线y=x+1经过圆心,且点P到直线y=x+1的距离为3=r,所以满足条件的点P的个数为2.
简答题
1、在△ABC中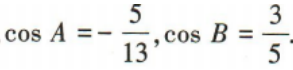 (1)求sinC的值;
(2)若AB=5,求BC的长.
(1)求sinC的值;
(2)若AB=5,求BC的长.
答 案:
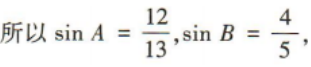
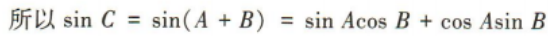
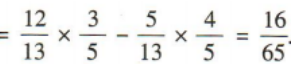

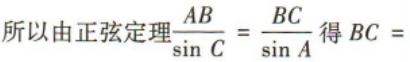
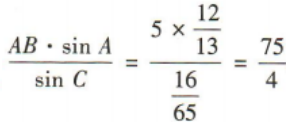
2、已知四边形 ABCD 为平行四边形,A(-2,1),B(4,0),D(-2,11).
(1)求点C的坐标;(2)若点P满足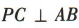 ,求直线 PC 的方程.
,求直线 PC 的方程.
答 案:(1)设点C的坐标为(a,b),则 因为四边形 ABCD 为平行四边形,
所以
因为四边形 ABCD 为平行四边形,
所以 所以
所以 解得
解得 所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率
所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率 设直线 PC 的方程为y= kx+b.
因为
设直线 PC 的方程为y= kx+b.
因为 所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.
所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.
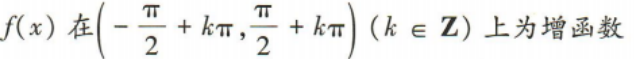
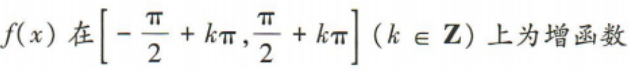

 上为增函数,但在整个定义域上不是单调函数.
上为增函数,但在整个定义域上不是单调函数.






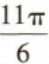
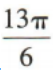
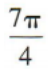
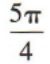

 时,函数y=ax与函数y=(a-1)x²+x在同一坐标系内的图象可能是()
时,函数y=ax与函数y=(a-1)x²+x在同一坐标系内的图象可能是() 



 ,位于y轴左侧,排除C选项.故选D.
,位于y轴左侧,排除C选项.故选D. 的解集为()(用区间表示)
的解集为()(用区间表示)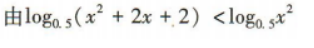
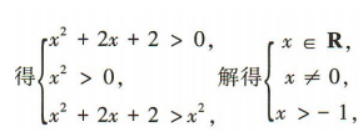

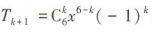 ,所以当k取1,3,5时,系数小于0.由组合数的性质知当日仅当k=3时,
,所以当k取1,3,5时,系数小于0.由组合数的性质知当日仅当k=3时,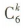 取最大值,所以当k=3时,系数取最小值,所以系数最小的项是第4项.
取最大值,所以当k=3时,系数取最小值,所以系数最小的项是第4项.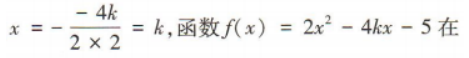

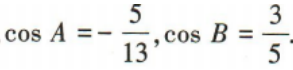 (1)求sinC的值;
(2)若AB=5,求BC的长.
(1)求sinC的值;
(2)若AB=5,求BC的长.
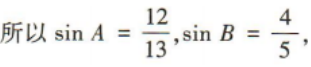
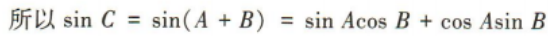
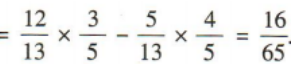

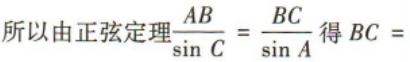
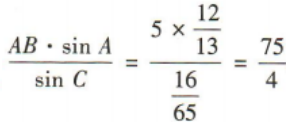
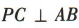 ,求直线 PC 的方程.
,求直线 PC 的方程.
 因为四边形 ABCD 为平行四边形,
所以
因为四边形 ABCD 为平行四边形,
所以 所以
所以 解得
解得 所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率
所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率 设直线 PC 的方程为y= kx+b.
因为
设直线 PC 的方程为y= kx+b.
因为 所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.
所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.



