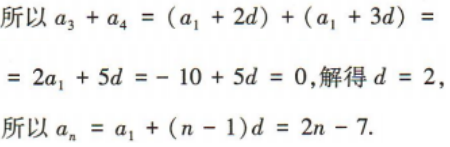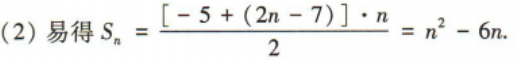2024年高职单招《数学(中职)》每日一练试题11月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知函数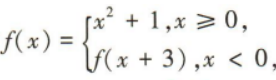 则f(-1)=()
则f(-1)=()
答 案:A
解 析: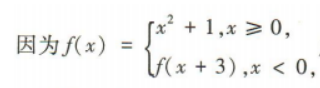
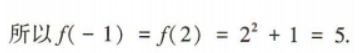
2、直线3x+4y-2=0与直线2x+y+2=0的交点坐标是()
- A:(2,2)
- B:(2,-2)
- C:(-2,2)
- D:(-2,-2)
答 案:C
解 析:由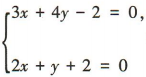 得
得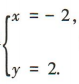 故所求交点坐标是(-2,2).
故所求交点坐标是(-2,2).
3、已知数列{an}为等比数列,若a1=8,a4=64,则公比q等于()
答 案:C
解 析:由题意得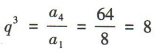 ,所以q=2。
,所以q=2。
4、315°=()
答 案:C
解 析:
填空题
1、若10件产品中有2件次品,现从中任取3件,则至少有一件是次品的取法共有()种。
答 案:64
解 析:从 10件产品中任取3件的取法共有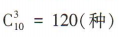 ,其中一件次品都没有的取法共有
,其中一件次品都没有的取法共有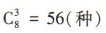 ,所以至少有一件次品的取法共有120-56=64(种).
,所以至少有一件次品的取法共有120-56=64(种).
2、已知数据x,8,y的平均数为8,则数据9,5,x,y,15 的平均数为()
答 案:9
解 析:因为x,8,y的平均数为8,所以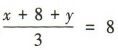 ,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为
,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为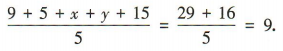
3、某同学6次技能测试的成绩分别是85,91,88,87,90,87,为了精确评价该同学技能发挥的稳定性,通过数据分析得到该组数据的标准差是()
答 案:2
解 析:由题意知该组数据的平均数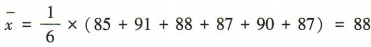 ,所以方差
,所以方差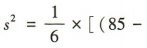
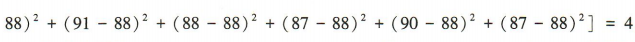 ,所以该组数据的标准差为
,所以该组数据的标准差为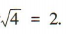
4、若点M(-1,2)在抛物线x2=2py(p>0)上,则该抛物线的方程为()
答 案: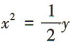
解 析:因为点M(-1,2)在抛物线x2= 2py上,所以(-1)2=4p,解得p=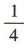 ,所以抛物线的方程为
,所以抛物线的方程为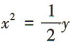
简答题
1、如图,在正方体ABCD-A1B1C1D1中.
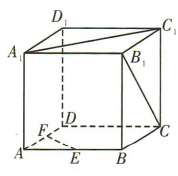 (1)求异面直线A1C1与B1C所成角的大小;
(1)求异面直线A1C1与B1C所成角的大小;
(2)若E,F分别为 AB,AD 的中点,求异面直线 A1C1与 EF 所成角的大小,
答 案: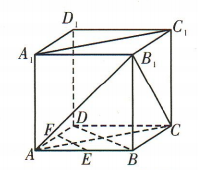 (1)如图所示,连接 AC,AB1
易得四边形 AA1C1C 为平行四边形,
∴AC//A1C1,
∴
(1)如图所示,连接 AC,AB1
易得四边形 AA1C1C 为平行四边形,
∴AC//A1C1,
∴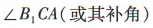 为A1C1与B1C所成的角,
易得
为A1C1与B1C所成的角,
易得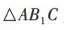 为等边三角形,
∴
为等边三角形,
∴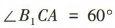 ,即AC与BC所成角的大小为 60°.
(2)连接 BD,如图.
由(1)知AC//A1C1.
∵E,F分别为 AB,AD 的中点:
∴EF//BD.
∴AC与BD所成的角就是A1C1与EF所成的角.
叉
,即AC与BC所成角的大小为 60°.
(2)连接 BD,如图.
由(1)知AC//A1C1.
∵E,F分别为 AB,AD 的中点:
∴EF//BD.
∴AC与BD所成的角就是A1C1与EF所成的角.
叉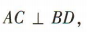 ∴
∴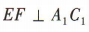 ,即A1C1与EF所成的角为 90°.
,即A1C1与EF所成的角为 90°.
2、已知S,是等差数列{an}的前n项和,a1=-5,a3+a4=0.
(1)求数列{an}的通项公式;
(2)若Sm=40,求m的值.
答 案:
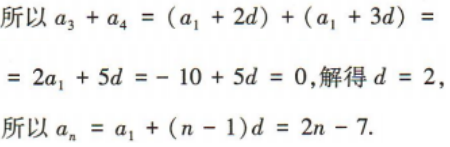
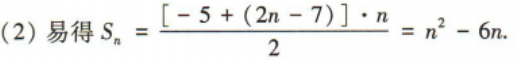

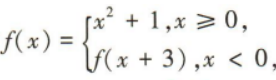 则f(-1)=()
则f(-1)=()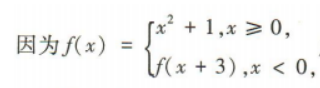
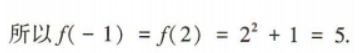
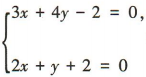 得
得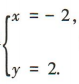 故所求交点坐标是(-2,2).
故所求交点坐标是(-2,2).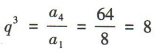 ,所以q=2。
,所以q=2。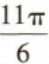
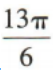
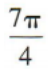
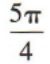

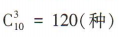 ,其中一件次品都没有的取法共有
,其中一件次品都没有的取法共有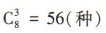 ,所以至少有一件次品的取法共有120-56=64(种).
,所以至少有一件次品的取法共有120-56=64(种).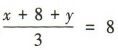 ,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为
,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为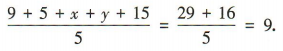
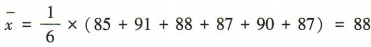 ,所以方差
,所以方差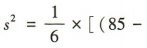
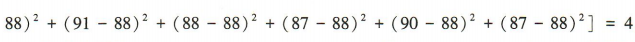 ,所以该组数据的标准差为
,所以该组数据的标准差为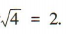
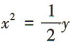
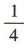 ,所以抛物线的方程为
,所以抛物线的方程为 (1)求异面直线A1C1与B1C所成角的大小;
(1)求异面直线A1C1与B1C所成角的大小; (1)如图所示,连接 AC,AB1
易得四边形 AA1C1C 为平行四边形,
∴AC//A1C1,
∴
(1)如图所示,连接 AC,AB1
易得四边形 AA1C1C 为平行四边形,
∴AC//A1C1,
∴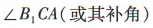 为A1C1与B1C所成的角,
易得
为A1C1与B1C所成的角,
易得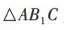 为等边三角形,
∴
为等边三角形,
∴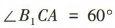 ,即AC与BC所成角的大小为 60°.
(2)连接 BD,如图.
由(1)知AC//A1C1.
∵E,F分别为 AB,AD 的中点:
∴EF//BD.
∴AC与BD所成的角就是A1C1与EF所成的角.
叉
,即AC与BC所成角的大小为 60°.
(2)连接 BD,如图.
由(1)知AC//A1C1.
∵E,F分别为 AB,AD 的中点:
∴EF//BD.
∴AC与BD所成的角就是A1C1与EF所成的角.
叉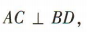 ∴
∴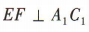 ,即A1C1与EF所成的角为 90°.
,即A1C1与EF所成的角为 90°.