2024年高职单招《数学(中职)》每日一练试题11月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设△ABC的内角A,B,C的对边分别为a,b,c,若a=2,c=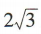 ,cosA=
,cosA=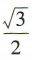 ,则b=()
,则b=()
- A:2
- B:2或4
- C:4
- D:
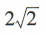
答 案:B
解 析:因为a²=b²+C²-2bccosA,a=2,c=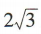 ,cosA=
,cosA=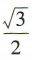 ,所以4=b²+12-6b,化简得b2-6b+8=0,解得b=2或b=4.
,所以4=b²+12-6b,化简得b2-6b+8=0,解得b=2或b=4.
2、已知集合A={1,a},B={1,2,3,4},且A∩B={1,4},则a的值为
答 案:D
解 析:因为A={1,a},B={1,2,3,4},A∩B={1,4},所以a=4.
3、已知幂函数f(x)=m2·xm在(0,+∞)上单调递增,则m=()
答 案:B
解 析: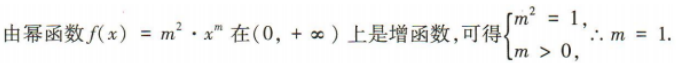
4、如图,从甲地到乙地有3条路,从乙地到丁地有2条路,从甲地到丙地有3条路,从丙地到丁地有4条路,则从甲地到丁地的不同路线(甲→乙→丁和甲→丙→丁)共有()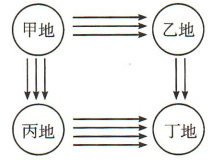
答 案:C
解 析:若路线为甲→乙→丁,则有3x2=6(条)不同路线,若路线为甲一丙一丁,则有3x4=12(条)不同路线.故甲地到丁地共有6+12=18(条)不同路线.
填空题
1、已知向量a=(4,3),b=(x,4),若a⊥b,则|b|=()
答 案:5
解 析:因为a⊥b,所以a·b=0.又a=(4,3),b=(x,4),所以4x+12=0,解得x=-3,所以b=(-3,4),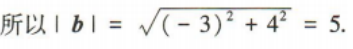
2、在△ABC中,内角A,B,C的对边分别是a,b,c,若A=60°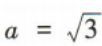 ,,则
,,则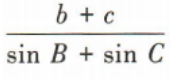 等于()
等于()
答 案:2
解 析: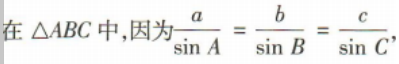
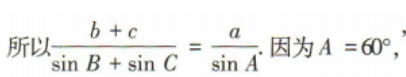
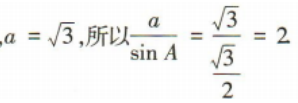
3、满足M∪{1}={0.1.2}的集合M的个数为()
答 案:2
解 析:因为M∪{1}={0,1,2},所以0,2必须是集合M中的元素,1可以是集合M中的元素,也可以不是集合M中的元素,所以M={0,2}或M={0,1,2},所以满足题意的M的个数是2.
4、生产某机器的总成本y(单位:万元)与产量x(单位:台)之间的函数关系式是y=x2-75x,若每台机器售价均为25万元,则该厂为使所获的利润最大应生产机器()台.
答 案:50
解 析:由题意可知生产x台机器获得的利润为25x-y=-x2+100x=-(x-50)2+2500.故当x=50时,获得利润最大.
简答题
1、制作一个高为20cm的长方体容器,底面矩形的长比宽长10cm,并且容积不少于4000cm3,问底面矩形的宽至少应是多少?
答 案:设底面矩形的宽为x cm. 由题意可得
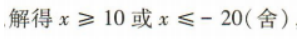 所以底面矩形的宽至少为10cm.
所以底面矩形的宽至少为10cm.
2、从2男2女4名羽毛球运动员中选出男女各一名配对参加混合双打,现从男女中各抽一人,求抽到男生甲的概率.
答 案:易知从男女中各抽一人的基本事件总数为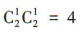 ,抽到男生甲的基本事件的个数为
,抽到男生甲的基本事件的个数为 ,
所以抽到男生甲的概率
,
所以抽到男生甲的概率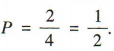
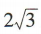 ,cosA=
,cosA=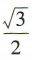 ,则b=()
,则b=()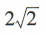
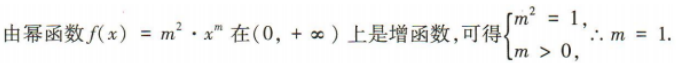

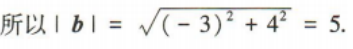
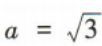 ,,则
,,则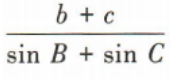 等于()
等于()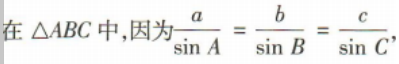
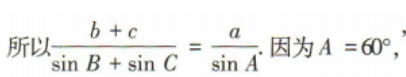
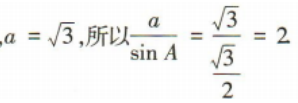

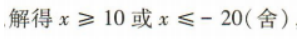 所以底面矩形的宽至少为10cm.
所以底面矩形的宽至少为10cm.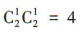 ,抽到男生甲的基本事件的个数为
,抽到男生甲的基本事件的个数为 ,
所以抽到男生甲的概率
,
所以抽到男生甲的概率