2024年高职单招《数学(中职)》每日一练试题11月06日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、若log2x=-3,则x=()
- A:-3
- B:9
- C:
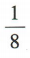
- D:
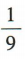
答 案:C
解 析:因为log2x=-3,所以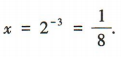
2、2022年北京冬奥会期间,需从5名志愿者中选3人去为速度滑冰、花样滑冰、冰球三个竞赛项目服务,每个项目必须有志愿者参加且每名志愿者只服务一个项目,则不同的安排方法种数为()
答 案:D
解 析:依题意知从5名志愿者中选3人服务3个不同项目,不同的安排方法有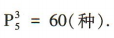
3、cos150°=()
答 案:A
解 析: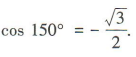
4、椭圆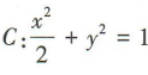 的离心率为()
的离心率为()
答 案:C
解 析:由椭圆C的方程,可知a=√2,b=1,所以c=√a²-b²=1,所以离心率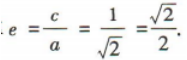
填空题
1、已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是()
答 案:a≥1
解 析:由A∪B=R,A={x|x<2a-1},B={x|x≥1}得2a-1≥1,解得a≥1.
2、直线y=x-1被圆C:x2+y2-4x=0所截得的弦长为()
答 案: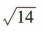
解 析:由x2+y2-4x=0得(x- 2)2+y2=4,所以圆C的圆心为(2,0),半径r=2,所以圆心C到直线y=x-1的距离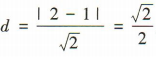 ,所以所求弦长为
,所以所求弦长为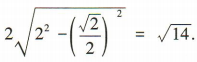
3、已知等差数列{an}的前n项和为Sn,且a1=16,a2=13,则S7=()
答 案:49
解 析:设等差数列{an}的公差为d.因为a1=16,a2=13,所以d=a2-a1=-3,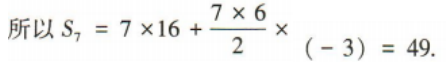
4、某医疗机构有4名新冠疫情防控志愿者,现要从这4人中选3个人去3个不同的社区进行志愿服务则不同的安排方法共有()种.
答 案:24
解 析:由题意可分两步,第一步,从4名新冠疫情防控志愿者中选出3人,共有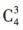 种方法:第二步,选出的3人去3 个不同的社区,共有
种方法:第二步,选出的3人去3 个不同的社区,共有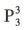 种方法,根据分步乘法计数原理可知不同的安排方法共有
种方法,根据分步乘法计数原理可知不同的安排方法共有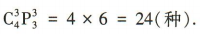
简答题
1、已知双曲线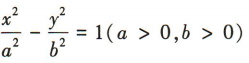 的右焦点为F2(3,0),渐近线方程为
的右焦点为F2(3,0),渐近线方程为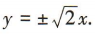 (1)求双曲线的标准方程;
(1)求双曲线的标准方程;
(2)过双曲线的右焦点,倾斜角为 30°的直线交双曲线于A,B两点,求|AB|.
答 案:(1)由题意的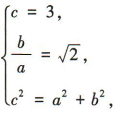 解得
解得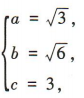 所以双曲线的标准方程为
所以双曲线的标准方程为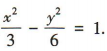 (2)设过双曲线的右焦点,倾斜角为 30°的直线为l.
易得直线l的斜率为
(2)设过双曲线的右焦点,倾斜角为 30°的直线为l.
易得直线l的斜率为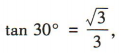 所以直线l的方程为
所以直线l的方程为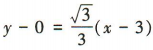 ,即
,即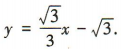 由
由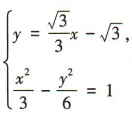 得5x2+6x-27=0.
易得△=62-4x5x(-27)>0.
设A(x1,y1),B(x2,y2),则
得5x2+6x-27=0.
易得△=62-4x5x(-27)>0.
设A(x1,y1),B(x2,y2),则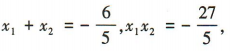 所以
所以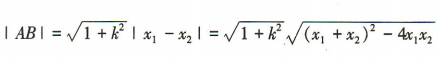
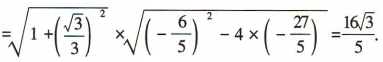
2、已知圆C:(x-2)2+(y-3)2= 4.
(1)圆外有一点P(4,-1),过点P作直线l与圆C相切,求直线l的方程;
(2)若直线x+y+m=0被圆C所截得的弦长为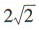 ,求m的值.
,求m的值.
答 案:(1)易知圆C:(x-2)2+(y-3)2= 4的圆心为(2,3),半径r= 2. 当直线l的斜率不存在时,直线l的方程为x=4,圆心到直线x=4的距离为2=r,符合题意.
当斜率存在时,设直线l的方程为kx-y-4k-1=0.
因为直线l与圆C相切,
所以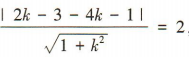 ,解得
,解得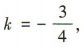 所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离
所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离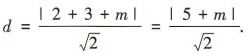 因为直线x+y+m=0被圆C所截得的弦长为
因为直线x+y+m=0被圆C所截得的弦长为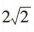 ,
所以
,
所以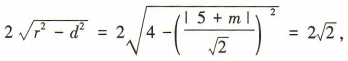 所以m=-3或m=-7.
所以m=-3或m=-7.
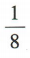
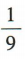
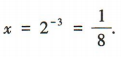
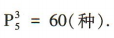
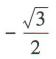
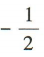
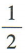
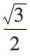
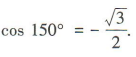
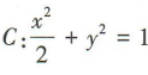 的离心率为()
的离心率为()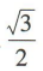
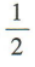
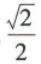
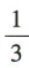
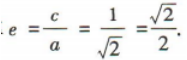
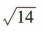
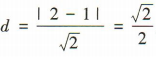 ,所以所求弦长为
,所以所求弦长为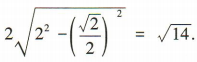
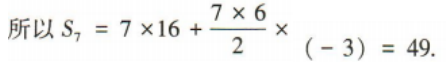
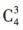 种方法:第二步,选出的3人去3 个不同的社区,共有
种方法:第二步,选出的3人去3 个不同的社区,共有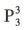 种方法,根据分步乘法计数原理可知不同的安排方法共有
种方法,根据分步乘法计数原理可知不同的安排方法共有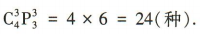
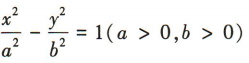 的右焦点为F2(3,0),渐近线方程为
的右焦点为F2(3,0),渐近线方程为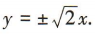 (1)求双曲线的标准方程;
(1)求双曲线的标准方程;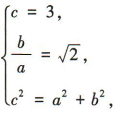 解得
解得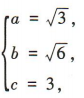 所以双曲线的标准方程为
所以双曲线的标准方程为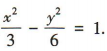 (2)设过双曲线的右焦点,倾斜角为 30°的直线为l.
易得直线l的斜率为
(2)设过双曲线的右焦点,倾斜角为 30°的直线为l.
易得直线l的斜率为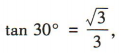 所以直线l的方程为
所以直线l的方程为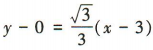 ,即
,即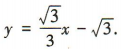 由
由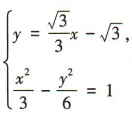 得5x2+6x-27=0.
易得△=62-4x5x(-27)>0.
设A(x1,y1),B(x2,y2),则
得5x2+6x-27=0.
易得△=62-4x5x(-27)>0.
设A(x1,y1),B(x2,y2),则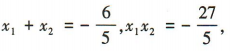 所以
所以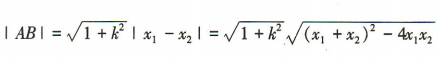
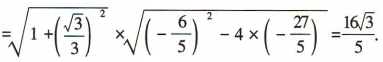
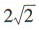 ,求m的值.
,求m的值.
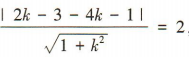 ,解得
,解得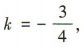 所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离
所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离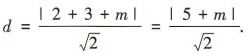 因为直线x+y+m=0被圆C所截得的弦长为
因为直线x+y+m=0被圆C所截得的弦长为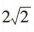 ,
所以
,
所以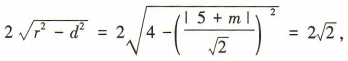 所以m=-3或m=-7.
所以m=-3或m=-7.


