2024年高职单招《数学(中职)》每日一练试题11月04日

2024年高职单招《数学(中职)》每日一练试题11月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若函数y=(a+1)x+b是增函数，则（）

• A：
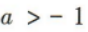
• B：
• C：
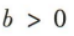
• D：

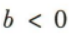
答 案：A

解 析：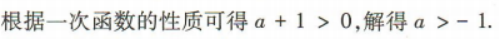

2、等比数列{an}中，首项a₁=8,公比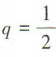,那么它的前5项和S₅的值为()  

• A：15.5
• B：20
• C：15
• D：20.75

答 案：A

解 析：在等比数列{an}中，由首项a₁=8,公比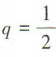得数列的前5项和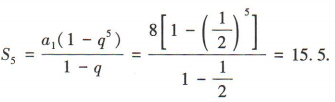

3、已知函数y=f(x)是偶函数，当x∈(0,+∞)时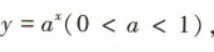，则该函数在(-∞,0)上的图像大致是（）

• A：
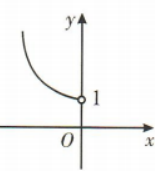
• B：
• C：
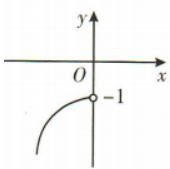
• D：

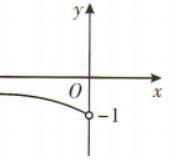
答 案：B

解 析：易知当x∈(0,+∞)时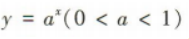， 为减函数，且函数值为正值.又y=f(x)是偶函数，所以y=f(x)在(-0,0)上为增函数，且函数值为正值.

4、不等式的正整数解有（）

• A：1个
• B：2个
• C：3个
• D：4个

答 案：B

解 析：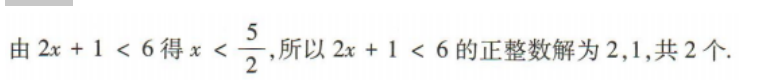

填空题

1、已知奇函数f(x)在[-3,0]上单调递减，且f(-3)=2,则f(x)在[0,3]上的最小值为（）

答 案：-2

解 析：因为f(x)为奇函数，且在[-3,0]上单调递减，所以f(x)在[0,3]上单调递减，所以f(x)在[0,3]上的最小值为f(3).由f(x)是奇函数，f(-3)=2得f(3)=-f(-3)=-2,所以f(x)在[0,3]上的最小值为-2

2、过点P(2,-1),且与直线3x-2y+5=0垂直的直线方程是()  

答 案：2x+3y-1=0

解 析：设与直线3x-2y+5=0垂直的直线方程为2x+3y+C=0,将点P(2,-1)代入可得2 x2+3x(-1)+C=0,解得C=-1,所以所求直线方程为 2x+3y-1= 0.

3、已知集合

答 案：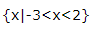

解 析：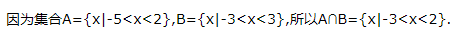

4、已知向量a=(1,0),b=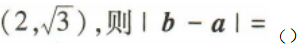

答 案：2

解 析：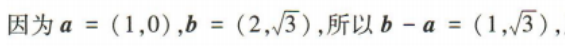

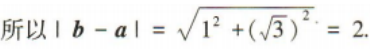
简答题

1、求不等式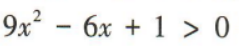的解集.  

答 案：

2、已知S_n是等差数列{a_n}的前n项和,a₆= 0,a₃+ a₇= 6 (1)求数列{an}的通项公式； (2)若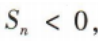求n的最小值.

答 案：(1)设等差数列{an}的公差为d. 因为a₆=0, 所以a₃+a₇=(a₆-3d)+(a₆+d)=-2d=6,解得d=-3, 所以a_n=a₆+(n-6)d=-3n+18.