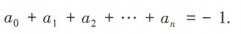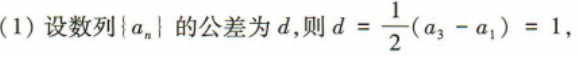2024年高职单招《数学(中职)》每日一练试题11月01日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设A,B 分别为椭圆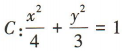 的左顶点和上顶点,F为C的右焦点,则F到直线AB的距离为()
的左顶点和上顶点,F为C的右焦点,则F到直线AB的距离为()
答 案:A
解 析:由题意可得A(-2,0),B(0,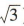 ),F(1,0),所以直线 A8 的方程为
),F(1,0),所以直线 A8 的方程为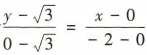 ,整理得
,整理得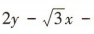
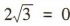 ,所以F到直线AB 的距离
,所以F到直线AB 的距离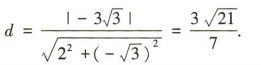
2、若a,b,c为实数,且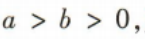 则下列结论错误的是()
则下列结论错误的是()
答 案:B
解 析: 故A不符合题意;当c=0时不等式不成立,故B符合题意;
故A不符合题意;当c=0时不等式不成立,故B符合题意;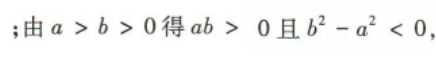
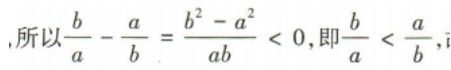 故C不符合题意;
故C不符合题意;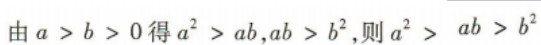 D不符合题意.
D不符合题意.
3、若集合A={0,1,2,3},B={1,2,4},则AUB=()
- A:{0,1,2,3,4}
- B:{1,2,3,4}
- C:{1,2}
- D:{0}
答 案:A
解 析:因为集合A={0,1,2,3}与B={1,2,4}的所有元素为0,1,2,3,4,所以AUB={0,1,2,3,4}.
4、函数f(x)=√3sinx-cosx的值域为()
- A:[-√3,√3]
- B:[-√3-1,√3+1]
- C:[-1,1]
- D:[-2,2]
答 案:D
解 析:易知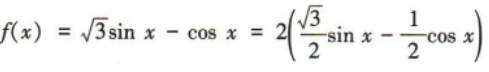
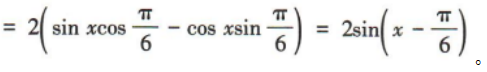 。因为
。因为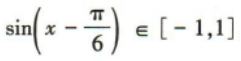
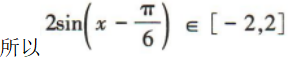 ,所以函数f(x)=√3sinx-cosx的值域为[-2,2].
,所以函数f(x)=√3sinx-cosx的值域为[-2,2].
填空题
1、如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=2,则二面角A-DD1-B的正切值为()

答 案: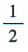
解 析:易得 ,
, 平面角.在
平面角.在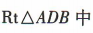 ,AB=1AD=2,
,AB=1AD=2,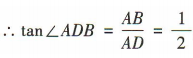 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为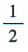 .
.
2、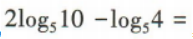 =()
=()
答 案:2
解 析: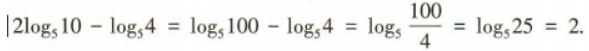
3、函数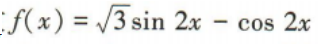 的最小正周期是()
的最小正周期是()
答 案:π
解 析: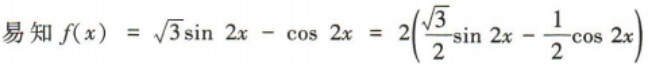

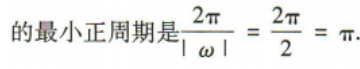
4、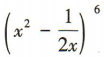 展开式中的常数项为()
展开式中的常数项为()
答 案: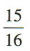
解 析:易知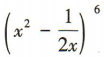 展开式的通项为
展开式的通项为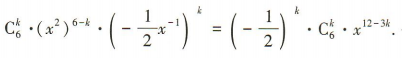 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以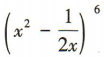 展开式中的常数项为
展开式中的常数项为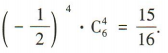
简答题
1、已知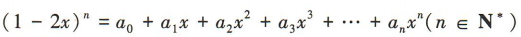 ,该展开式的二项式系数之和为 32. (1)求n的值;(2)求
,该展开式的二项式系数之和为 32. (1)求n的值;(2)求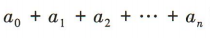 的值.
的值.
答 案:(1)因为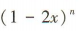 的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得
的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得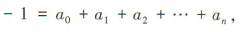 所以
所以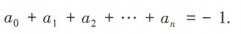
2、已知数列{an}是等差数列,a1=1,a3=3.
(1)求数列{an}的通项公式;
(2)设bn=(-1)nan,数列{bn}的前n项和为Tn,求T100
答 案: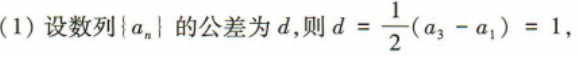

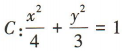 的左顶点和上顶点,F为C的右焦点,则F到直线AB的距离为()
的左顶点和上顶点,F为C的右焦点,则F到直线AB的距离为()
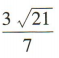



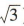 ),F(1,0),所以直线 A8 的方程为
),F(1,0),所以直线 A8 的方程为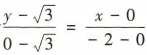 ,整理得
,整理得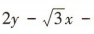
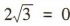 ,所以F到直线AB 的距离
,所以F到直线AB 的距离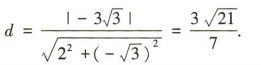
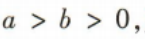 则下列结论错误的是()
则下列结论错误的是()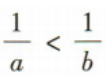
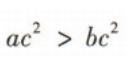
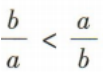
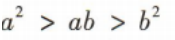
 故A不符合题意;当c=0时不等式不成立,故B符合题意;
故A不符合题意;当c=0时不等式不成立,故B符合题意;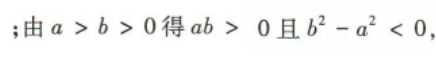
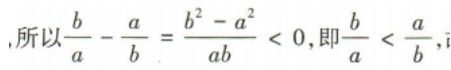 故C不符合题意;
故C不符合题意;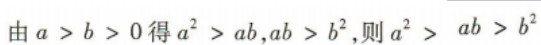 D不符合题意.
D不符合题意.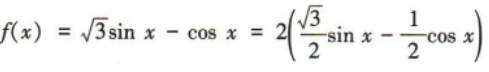
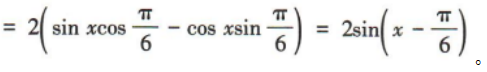 。因为
。因为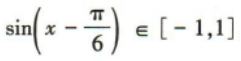
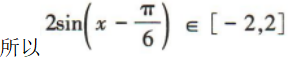 ,所以函数f(x)=√3sinx-cosx的值域为[-2,2].
,所以函数f(x)=√3sinx-cosx的值域为[-2,2].
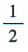
 ,
, 平面角.在
平面角.在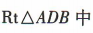 ,AB=1AD=2,
,AB=1AD=2,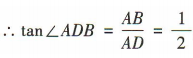 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为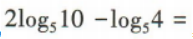 =()
=()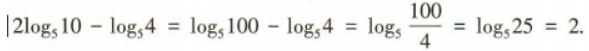
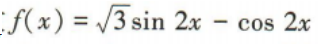 的最小正周期是()
的最小正周期是()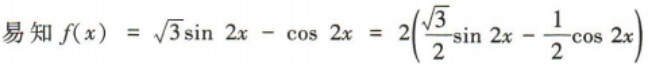

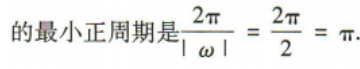
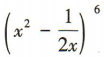 展开式中的常数项为()
展开式中的常数项为()
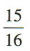
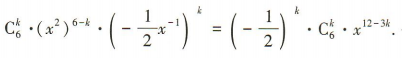 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以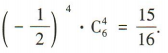
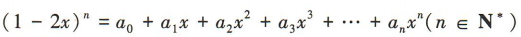 ,该展开式的二项式系数之和为 32. (1)求n的值;(2)求
,该展开式的二项式系数之和为 32. (1)求n的值;(2)求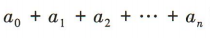 的值.
的值. 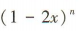 的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得
的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得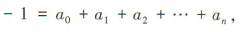 所以
所以