课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年高职单招《数学(中职)》每日一练试题10月31日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、命题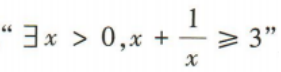 的否定是()
的否定是()
答 案:C
解 析:因为命题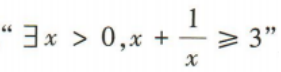 是特称命题,所以其否定是全称命题,即
是特称命题,所以其否定是全称命题,即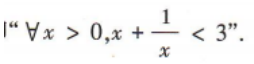
2、把曲线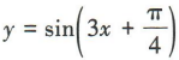 向右平移
向右平移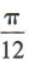 个单位长度,所得曲线的函数解析式为()
个单位长度,所得曲线的函数解析式为()
答 案:A
解 析:将曲线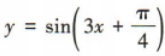 向右平移
向右平移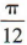 个单位长度,得到
个单位长度,得到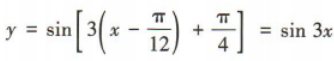 的图象,所以所得曲线的函数解析式为y=sin3x.
的图象,所以所得曲线的函数解析式为y=sin3x.
3、函数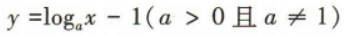 的图像过定点()
的图像过定点()
- A:(0,-1)
- B:(1,-1)
- C:(1,1)
- D:(1,0)
答 案:B
解 析:令x=1,则y=loga1-1=-1,所以函数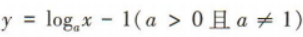 的图像过定点(1,-1).
的图像过定点(1,-1).
4、已知函数f(x)=x2+ax+2在区间(-∞,1]内单调递减,则实数a的取值范围是()
答 案:A
解 析:易得函数f(x)=x2+ax+2的图像开口向上,对称轴为直线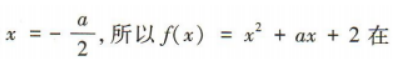



填空题
1、若2a=3,b=log34,则ab=()
答 案:2
解 析: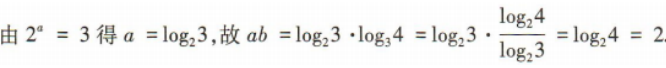
2、如图,画一个边长为4的正方形,再将这个正方形各边的中点相连得到第2个正方形,依此类推,这样一共画了10个正方形,则第10个正方形的面积为()

答 案: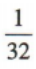
解 析:由题意知,第一个正方形的边长a1=4,面积T1=16;第二个正方形的边长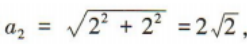 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长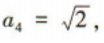 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
3、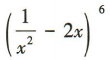 的展开式中各项系数之和为()
的展开式中各项系数之和为()
答 案:1
解 析:令x=1,得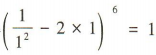 ,即
,即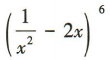 的展开式中各项系数之和为1.
的展开式中各项系数之和为1.
4、若双曲线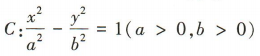 的虚轴长为8,渐近线方程为
的虚轴长为8,渐近线方程为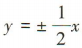 ,则双曲线C的方程为()
,则双曲线C的方程为()
答 案: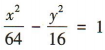
解 析:由题可得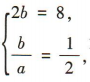 解得
解得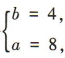 所以双曲线的方程为
所以双曲线的方程为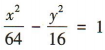
简答题
1、已知p:x2-8x-20≤0,q:1-m≤x≤1+m(m>0).若p是q的必要不充分条件,求实数m的范围.
答 案:由x2-8x-20≤0得-2≤x≤10,即p:-2≤x≤10. ∵p是q的必要不充分条件,q:1-m≤x≤1+m(m>0),
2、若一元二次不等式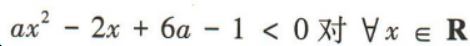 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
答 案: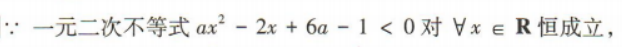

温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
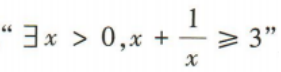 的否定是()
的否定是()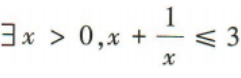
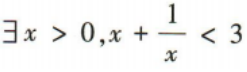
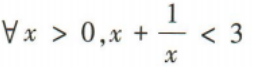
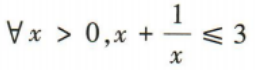
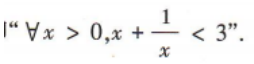
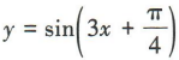 向右平移
向右平移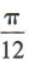 个单位长度,所得曲线的函数解析式为()
个单位长度,所得曲线的函数解析式为()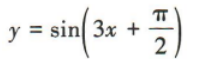
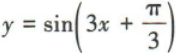
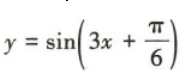
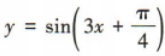 向右平移
向右平移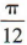 个单位长度,得到
个单位长度,得到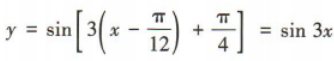 的图象,所以所得曲线的函数解析式为y=sin3x.
的图象,所以所得曲线的函数解析式为y=sin3x.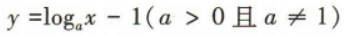 的图像过定点()
的图像过定点()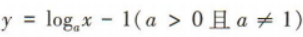 的图像过定点(1,-1).
的图像过定点(1,-1).




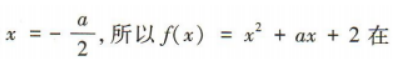



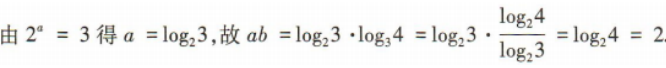

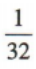
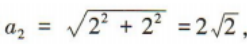 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长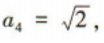 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
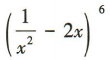 的展开式中各项系数之和为()
的展开式中各项系数之和为()
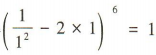 ,即
,即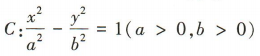 的虚轴长为8,渐近线方程为
的虚轴长为8,渐近线方程为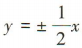 ,则双曲线C的方程为()
,则双曲线C的方程为()
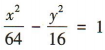
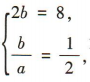 解得
解得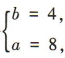 所以双曲线的方程为
所以双曲线的方程为
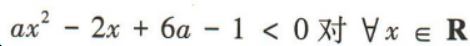 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.