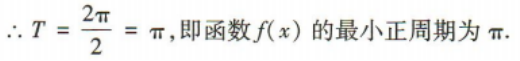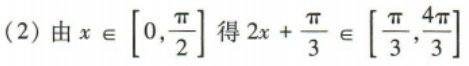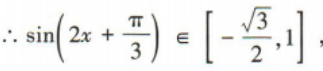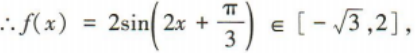2024年高职单招《数学(中职)》每日一练试题10月30日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列与集合{2 023,1}表示同一集合的是()
- A:( 2 023,1)
- B:{(x,y)|x=2 023,y=1}
- C:{x|x2-2 024x+2 023=0}
- D:{(2 023,1)}
答 案:C
解 析:方程x2-2 024x+2 023=0的解为x=2 023或x=1,所以|x|x2-2 024x+2 023=0}={2 023,1}, 故{x|x2-2 024x+2 023=0}与集合{2 023,1}表示同一集合.
2、若指数函数y=(a+1)x是增函数,则a的取值范围是()
- A:(-1,0]
- B:(-1,0)
- C:(0,+∞)
- D:[0,+∞)
答 案:C
解 析:因为指数函数y=(a+1)x是增函数。
3、在等比数列{an}中,若a3a5=16,则a4=()
答 案:D
解 析: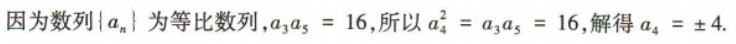
4、函数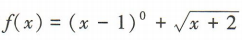 的定义域为()
的定义域为()
- A:(-2,1)
- B:[-2,+∞)
- C:[-2,1)U(1,+∞)
- D:(1,+∞)
答 案:C
解 析:要使函数f(x)有意义,须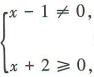 解得x≥-2且x≠1,所以f(x)的定义域为[-2,1)U(1,+∞).
解得x≥-2且x≠1,所以f(x)的定义域为[-2,1)U(1,+∞).
填空题
1、(2+x)6展开式中含x3项的二项式系数为()
答 案:20
解 析:(2+x)6展开式中含x3项的二项式系数为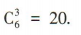
2、已知平面向量a=(-3,m),b=(m-2,-1),若a与b的方向相反,则实数m的值为()
答 案:3
解 析: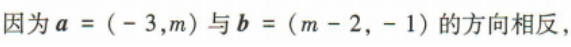
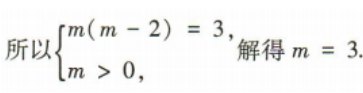
3、过点P(2,-1),且与直线3x-2y+5=0垂直的直线方程是()
答 案:2x+3y-1=0
解 析:设与直线3x-2y+5=0垂直的直线方程为2x+3y+C=0,将点P(2,-1)代入可得2 x2+3x(-1)+C=0,解得C=-1,所以所求直线方程为 2x+3y-1= 0.
4、函数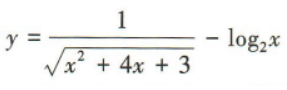 的定义域为()
的定义域为()
答 案:(0,+∞)
解 析: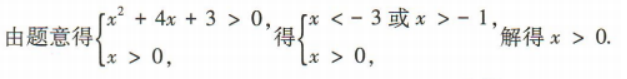
简答题
1、如图,已知 A,B,C,D是空间中四点,且点A,B,C在同一直线l上,点D不在直线l上,证明直线 AD,BD,CD在同一平面内.
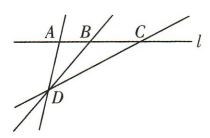
答 案:因为点A,B,C在同一直线l上,点D不在直线l上,过直线与直线外一点有且只有一个平面, 所以点 A,B,C,D确定唯一的一个平面,设为α,
所以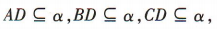 所以直线 AD,BD,CD 在同一平面内.
所以直线 AD,BD,CD 在同一平面内.
2、已知函数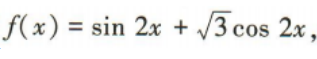 x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在
x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在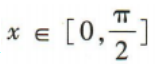 上的最值.
上的最值.
答 案:
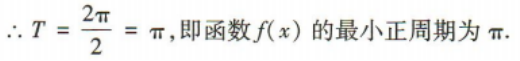
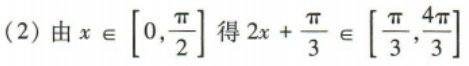
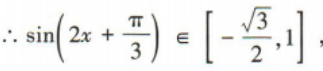
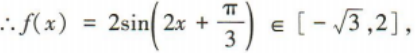


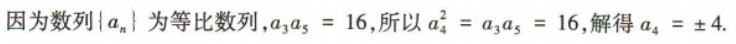
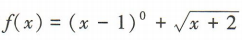 的定义域为()
的定义域为()
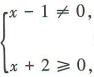 解得x≥-2且x≠1,所以f(x)的定义域为[-2,1)U(1,+∞).
解得x≥-2且x≠1,所以f(x)的定义域为[-2,1)U(1,+∞).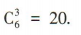
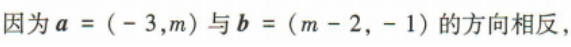
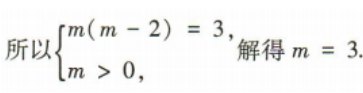
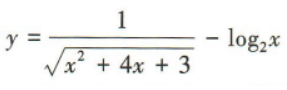 的定义域为()
的定义域为()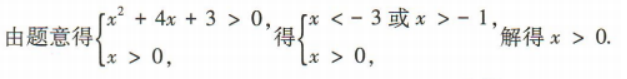

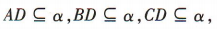 所以直线 AD,BD,CD 在同一平面内.
所以直线 AD,BD,CD 在同一平面内.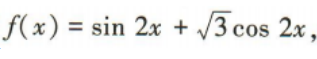 x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在
x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在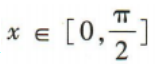 上的最值.
上的最值.