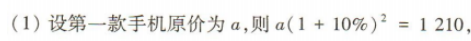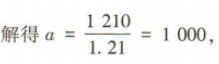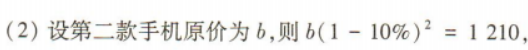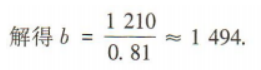2024年高职单招《数学(中职)》每日一练试题10月29日

2024年高职单招《数学(中职)》每日一练试题10月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知函数f(x)是定义在R上的奇函数，且对于任意实数x,都有f(x+4)=f(x),若f(-1)=3,则f(4)+f(5)=（）  

• A：-3
• B：0
• C：3
• D：6

答 案：A

解 析：因为f(x)是定义在R上的奇函数，所以f(0)=0,f(1)=-f(-1)=-3.又f(x+4)=f(x),所以f(4)= f(0)=0,f(5)=f(1)=-3,所以f(4)+f(5)=-3  

2、已知函数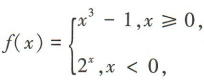设f(0)=a,则f(a)=（）  

• A：-2
• B：-1
• C：
• D：0

答 案：C

解 析：∵函数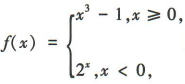且0≥0,:.f(0)=0³-1=-1=a,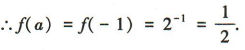

3、若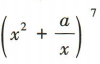的展开式中的各项系数之和为-1,则a的值为（）  

• A：1
• B：-1
• C：2
• D：-2

答 案：D

解 析：令x= 1,得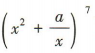的展开式中的各项系数之和为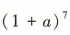,所以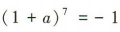,解得a=-2.

4、以(0,-1)为圆心,2为半径的圆的标准方程是（）  

• A：x²+(y+1)²=2
• B：x²+(y+1)²=4
• C：(x+1)²+y²=2
• D：(x+1)²+y²=4

答 案：B

解 析：以(0,-1)为圆心,2为半径的圆的标准方程是x²+(y+1)²=4.

填空题

1、已知{a_n}为等差数列，且a₄+a₈+a₁₀=50,则a₂+2a₁₀=（）

答 案：50

解 析：由数列{an}为等差数列得a₄+a₈+a₁₀=a₂+a₈+a₁₂=a₂+2a₁₀=50

2、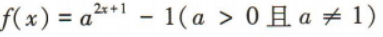的图像过定点（）

答 案：

解 析：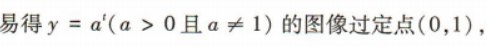

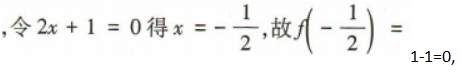
3、已知角α的顶点与坐标原点重合，始边与x轴正半轴重合，终边经过点P(x,-3),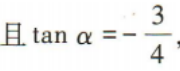 sinα的值为（）

答 案：

解 析：

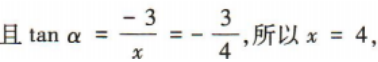
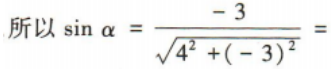
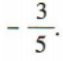
4、已知函数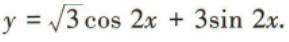 求： (1)函数的值域； (2)函数的最小正周期； (3)函数取得最大值时x的取值集合.

答 案：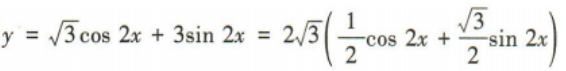

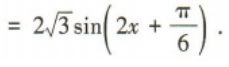
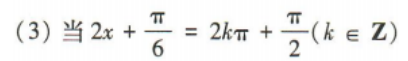
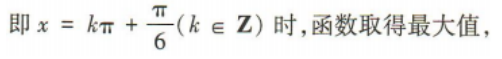
简答题

1、求不等式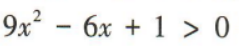的解集.  

答 案：

2、某商场出售两款型号不同的手机，由于市场需求发生变化，第一款手机连续两次提价10%,第二款手机连续两次降价10%,结果都以1 210元出售 (1)求第一款手机的原价； (2)若该商场同时出售两款手机各一部，求总售价与总原价之间的差额.(结果保留整数)

答 案：