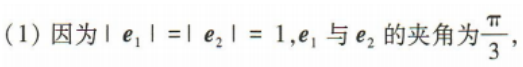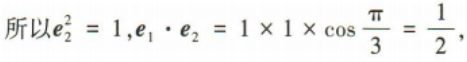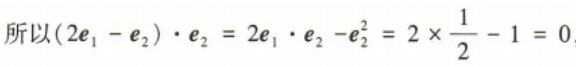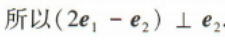2024年高职单招《数学(中职)》每日一练试题10月27日
2024-10-27 15:59:01 来源：吉格考试网
2024年高职单招《数学(中职)》每日一练试题10月27日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、已知一个圆锥的母线长为6,侧面积为18π,则此圆锥的体积为()
- A：9π
- B：12π
- C：
- D：
答 案：C
解 析：设圆锥的底面半径为r,高为h,则π×6×r=18π,解得r=3,所以圆锥的高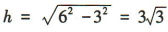
,所以该圆锥的体积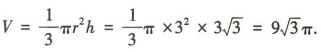
2、已知集合A={-1,0,1},B={0,1},则AUB=()
- A：{0,1}
- B：{-1,0}
- C：{-1,0,1}
- D：{-1,1}
答 案：C
解 析：因为集合A={-1,0,1},B={0,1},所以AUB={-1,0,1}.
3、已知点A(0,-1),B(2,3),点P满足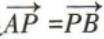
,则点P的坐标为（）
- A：(2,2)
- B：(1,1)
- C：(2,4)
- D：(1,2)
答 案：B
解 析：
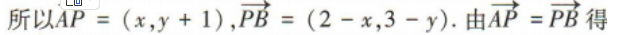
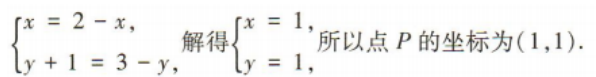
4、已知数列{an}是等差数列，且a2+a10=4,则log2a6=（）
- A：0
- B：1
- C：2
- D：3
答 案：B
解 析：由等差中项的性质可得2a6=a2+a10=4,即a6=2,所以log2a6=1.
填空题
1、(x-2)6的展开式中x4的系数为()
答 案：60
解 析：(x-2)6的展开式的通项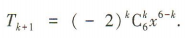
令6-k=4，可得k=2.则x4的系数是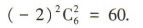
2、设ω为实数，函数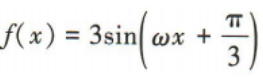
的最小正周期为
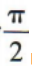则ω的值为（）
答 案：±4
解 析：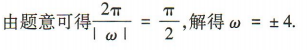
3、已知函数f(x)在[3-2a,a]上是偶函数，则实数a=（）
答 案：3
解 析：由题意得3-2a+a=0,解得a=3.
4、已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=（）
答 案：2
解 析：∵A∩B={2,3},所以2∈B,又B={a,3,4},∴a=2.
简答题
1、已知i为虚数单位,实数x与y满足(x+y)-xyi=-5+24i,求x与y的值.
答 案：由题意得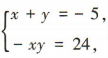
解得
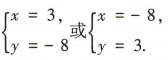
2、已知单位向量
(1)证明(2e1-e2)⊥e2;
(2)若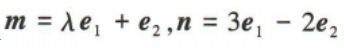
,且|m|=|n|,求λ的值
答 案：
- 备考交流
-
单招真题交流3群
扫一扫或点击二维码入群
