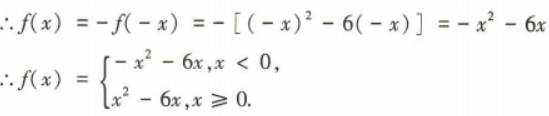2024年高职单招《数学(中职)》每日一练试题10月26日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、不等式的解集是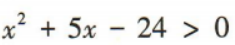
答 案:A
解 析:易知方程x2+5x-24=0的两根分别为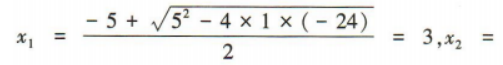
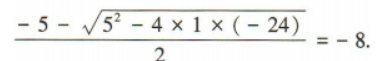

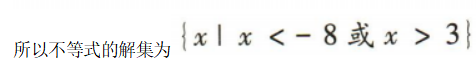
2、若双曲线的一个焦点坐标为F(-2,0),右顶点的坐标为(1,0),则双曲线的标准方程是()
答 案:A
解 析:因为焦点在x轴上,所以设双曲线的标准方程为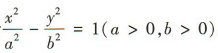 ,由题意可知c= 2,a=1,所以 b2=c2-a2=3,所以双曲线的标准方程为
,由题意可知c= 2,a=1,所以 b2=c2-a2=3,所以双曲线的标准方程为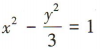
3、函数 的定义域是()
的定义域是()
- A:[2,+∞)
- B:(2,+∞)
- C:(-∞,2]
- D:(-∞,2)
答 案:A
解 析: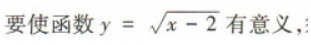

4、双曲线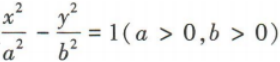 的左、右焦点分别为F1,F2,右顶点为A,若
的左、右焦点分别为F1,F2,右顶点为A,若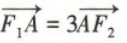 ,则该双曲线的离心率为()
,则该双曲线的离心率为()
答 案:C
解 析:设双曲线的焦距为2c.由题意可知F1(-c,0),F2(c,0),A(a,0),所以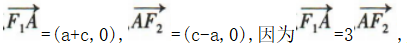
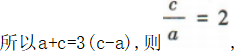 即双曲线的离心率为2
即双曲线的离心率为2
填空题
1、在正方体 ABCD-A1B1C1D1中,直线 A1B 与平面 ABCD 所成角的大小为()
答 案:45°
解 析:易得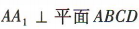 ,所以
,所以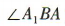 为A1B与平面ABCD所成的角.因为
为A1B与平面ABCD所成的角.因为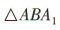 为等腰直角三角形,且
为等腰直角三角形,且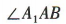 = 90°,所以
= 90°,所以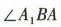 = 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
= 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
2、将某校100名学生的数学测试成绩绘制成如图所示的频率分布直方图,分数不低于a(a为整数)为优秀,如果优秀的人数为20,则a的估计值是()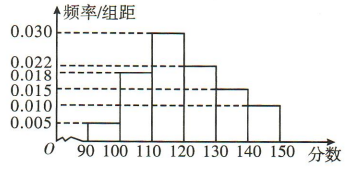
答 案:133
解 析:分数低于140的人数为100x10x(0.005+0.018+0.030+0.022+0.015)= 90.分数低于130的人数为100 x10x(0.005 +0.018 + 0.030+0.022)= 75,故a∈(130,140),所以[(140-a) x0. 015 + 0.01 x 10]x100=20.解得a≈133.
3、盒子中有散落的黑白棋子若干粒,已知从中取出2粒都是黑子的概率是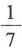 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是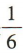 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
答 案: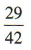
解 析:由题意,任意取出2粒棋子,不考虑先后顺序,一共有2粒都是黑子,2粒都是白子和一粒黑子一粒白子3 种可能.设事件A =“取出2粒都是黑子”,事件B=“取出2粒都是白子”,事件C=“取出2粒恰好是一粒黑子一粒白子”,则A,B,C两两互斥.由已知得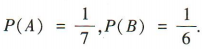 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=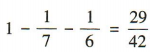 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是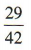
4、在等比数列{an}中,a1=1,a2=3,则a5=()
答 案:81
解 析:
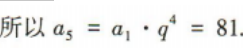
简答题
1、已知向量a=(1,x),b=(2x+3,-x).
(1)若a//b,求|a-b|;
(2)若a与b的夹角为锐角,求x的取值范围.
答 案:(1)因为a=(1,x),b=(2x+3,-x),a//b, 所以-x=x(2x+3),解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),
所以a-b=(-2,0),
所以|a-b|=2;
当x=-2时,a=(1,-2),b=(-1,2),
所以a-b=(2,-4),
所以|a-b|=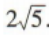 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=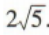 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
2、已知函数f(x)是定义在R上的奇函数,且当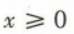 时,f(x)=x2-6x.
(1)画出f(x)的图像;
时,f(x)=x2-6x.
(1)画出f(x)的图像;
 (2)根据图像直接写出f(x)的单调递增区间;
(3)写出f(x)的解析式.
(2)根据图像直接写出f(x)的单调递增区间;
(3)写出f(x)的解析式.
答 案:(1)作出f(x))的图像如图所示.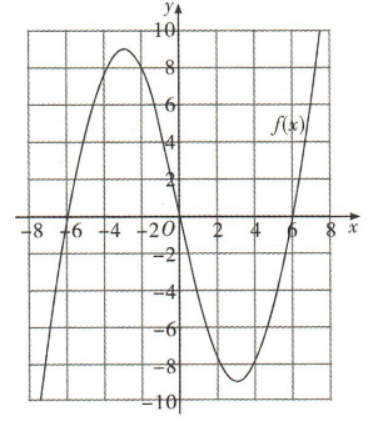

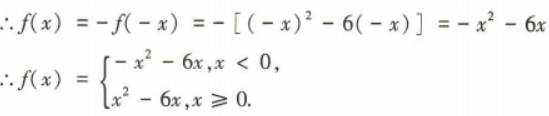
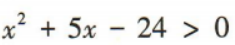
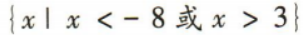

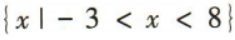
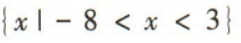
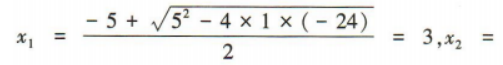
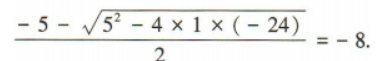

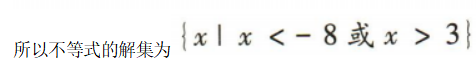
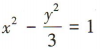
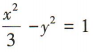
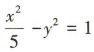
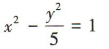
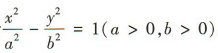 ,由题意可知c= 2,a=1,所以 b2=c2-a2=3,所以双曲线的标准方程为
,由题意可知c= 2,a=1,所以 b2=c2-a2=3,所以双曲线的标准方程为 的定义域是()
的定义域是()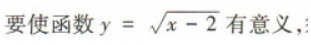

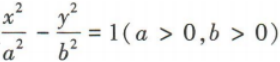 的左、右焦点分别为F1,F2,右顶点为A,若
的左、右焦点分别为F1,F2,右顶点为A,若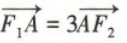 ,则该双曲线的离心率为()
,则该双曲线的离心率为()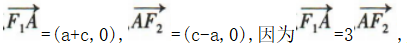
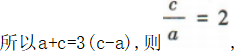 即双曲线的离心率为2
即双曲线的离心率为2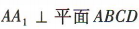 ,所以
,所以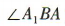 为A1B与平面ABCD所成的角.因为
为A1B与平面ABCD所成的角.因为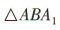 为等腰直角三角形,且
为等腰直角三角形,且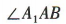 = 90°,所以
= 90°,所以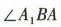 = 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
= 45°,所以直线 A1B 与平面 ABCD 所成的角为 45°.
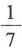 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是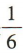 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
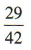
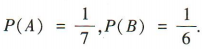 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=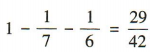 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是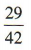

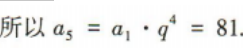
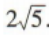 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=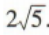 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).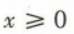 时,f(x)=x2-6x.
(1)画出f(x)的图像;
时,f(x)=x2-6x.
(1)画出f(x)的图像;
 (2)根据图像直接写出f(x)的单调递增区间;
(3)写出f(x)的解析式.
(2)根据图像直接写出f(x)的单调递增区间;
(3)写出f(x)的解析式.