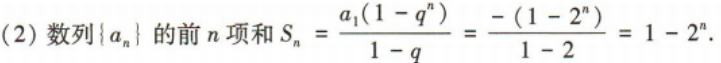2024年高职单招《数学(中职)》每日一练试题10月23日

2024年高职单招《数学(中职)》每日一练试题10月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、cos105°cos45°+sin105°sin45°=()  

• A：
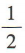
• B：
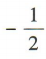
• C：
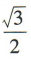
• D：

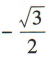
答 案：A

解 析：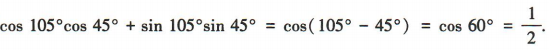

2、924°是（）  

• A：第一象限角
• B：第二象限角
• C：第三象限角
• D：第四象限角

答 案：C

解 析：因为924°=3×360°-156°,所以924°角与-156°角的终边相同，又-156°角的终边在第三象限，所以924°是第三象限角.

3、已知角α的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(2,-3),则cosα=()  

• A：
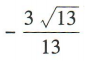
• B：
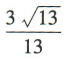
• C：
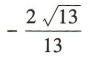
• D：

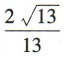
答 案：D

解 析：因为角α的终边经过点P(2,-3),所以P到原点0的距离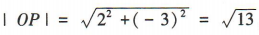,所以cosα=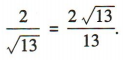

4、已知α为第二象限角，则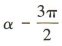为()  

• A：第一象限角
• B：第二象限角
• C：第三象限角
• D：第四象限角

答 案：C

解 析：因为α为第二象限角，所以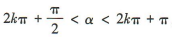,k∈Z,所以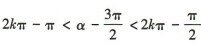,k∈Z,所以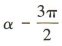为第三象限角.

填空题

1、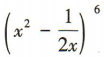展开式中的常数项为（）  

答 案：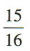

解 析：易知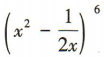展开式的通项为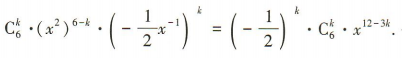令12-3k =0,解得k=4,所以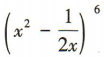展开式中的常数项为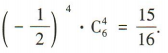

2、若向量a=(-2,1),b=(1,3),c=a+2b,则c=（）

答 案：（0,7）

解 析：由a=(-2,1),b=(1,3),得c=a+2b=(0,7).

3、在长方体ABCD-A₁B₁C₁D₁中,AB=4,BC=3,BB₁=2,那么 BC 到平面 ADD₁A₁的距离为()  

答 案：4

解 析：易得BC//平面ADD₁A₁,所以点B到平面ADD₁A₁的距离为BC到平面ADD₁A₁的距离.因为,所以AB的长为BC到平面ADD₁A₁的距离.又AB=4,所以BC到平面 ADD₁A₁的距离为 4.

4、双曲线 25x²-16y²=400 的渐近线方程为()  

答 案：5x±4y =0

解 析：将双曲线方程25x²-16y²=400化为标准方程为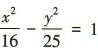,所以双曲线25x²-16y²=400的渐近线方程为5x±4y=0.

简答题

1、在长为8m,宽为6m的矩形地面的四周种植花卉，中间种植草坪.如果要求花卉带的宽度相同，且草坪的面积不超过总面积的一半，那么花卉带的宽度应为多少米?

答 案：设花卉带的宽度应为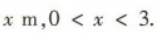

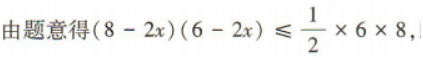
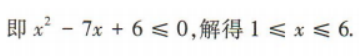
2、在等比数列{an}中,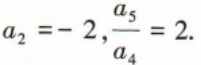 (1)求{an}的通项公式； (2)求数列{an}的前n项和Sn.

答 案：