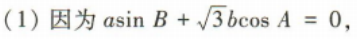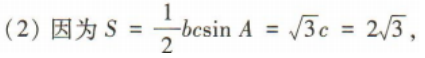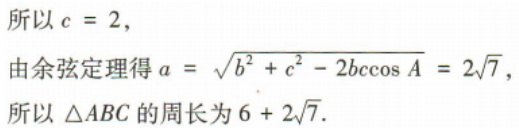2024年高职单招《数学(中职)》每日一练试题10月22日
2024-10-22 16:21:03 来源:吉格考试网
2024年高职单招《数学(中职)》每日一练试题10月22日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、椭圆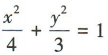 的焦点坐标为()
的焦点坐标为()
- A:(5,0),(-5,0)
- B:(1,0),(-1,0)
- C:
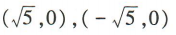
- D:
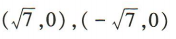
答 案:B
解 析:易得椭圆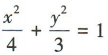 的半焦距
的半焦距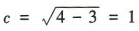 ,则焦点坐标为(1,0),(-1,0).
,则焦点坐标为(1,0),(-1,0).
2、设f(x)是定义在R上的偶函数,且在区间(-∞,0]上为增函数.若f(-1)=0,则使得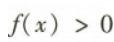 的x的取值范围是()
的x的取值范围是()
- A:(-∞,-1)
- B:(-1,1)
- C:(1,+∞)
- D:(-∞,-1)∪(1,+∞)
答 案:B
解 析:因为f(x)在(-∞,0]上是增函数且f(-1)=0,所以当x∈(-1,0)时,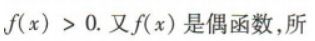

3、已知双曲线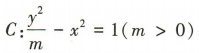 的离心率
的离心率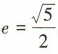 ,则双曲线C的渐近线方程为()
,则双曲线C的渐近线方程为()
- A:y=±2x
- B:
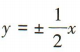
- C:
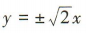
- D:
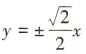
答 案:A
解 析:由双曲线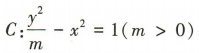 可得 α2= m,b2 =1 因为双曲线C的离心率
可得 α2= m,b2 =1 因为双曲线C的离心率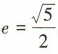 ,所以
,所以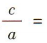
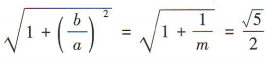 解得m =4,所以a=2,所以双曲线C的渐近线方程为
解得m =4,所以a=2,所以双曲线C的渐近线方程为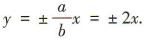
4、在正方体ABCD-A1B1C1D1中,异面直线AA1与BC所成的角是()
- A:30°
- B:45°
- C:60°
- D:90°
答 案:D
解 析:在正方体ABCD-A1B1C1D1中,∵AA1⊥平面ABCD,BC⊂平面ABCD,∴AA1⊥BC,∴异面直线AA1与BC所成的角是90°.
填空题
1、将2.5.11三个数分别加上相同的常数m.使得到的三个数依次成等比数列,则m=()
答 案:1
解 析:2+m,5+m,11+m三个数依次成等比数列,所以(5+m)2=(2+m)(11+m),解得m=1.
2、已知集合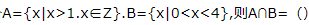
答 案:{2,3}
解 析:因为A={x|x>1,x∈Z}={2,3,4,…},B={x|0 3、在△ABC中,内角A,B,C的对边分别为a,b,c,且c=3,sinB=2sinA,且 答 案: 4、某同学6次技能测试的成绩分别是85,91,88,87,90,87,为了精确评价该同学技能发挥的稳定性,通过数据分析得到该组数据的标准差是()
答 案:2 解 析:由题意知该组数据的平均数 简答题 1、已知椭圆 答 案:(1)易得抛物线y2= 4x的焦点为F2(1,0), 所以椭圆的左焦点为F1(-1,0).
又直线 MN 的斜率 2、在△ABC中,角A,B,C的对边分别为a,b,c,且 答 案: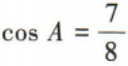 b≠c
(1)求b的值;
(2)求△ABC的面积.
b≠c
(1)求b的值;
(2)求△ABC的面积.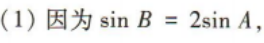
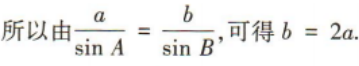
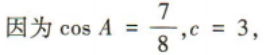


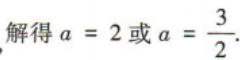
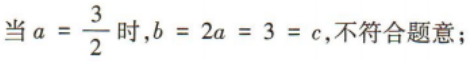
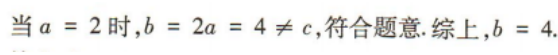

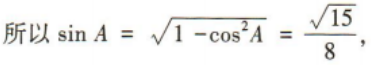

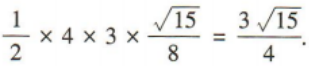
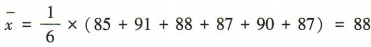 ,所以方差
,所以方差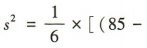
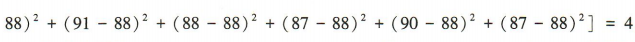 ,所以该组数据的标准差为
,所以该组数据的标准差为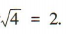
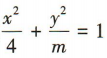 与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为
与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为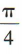 的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
(2)求△OMN的面积(O为坐标原点)
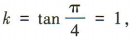 所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为
所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为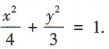 (2)设M,N的坐标分别为(x1,y1),(x2,y2).
由
(2)设M,N的坐标分别为(x1,y1),(x2,y2).
由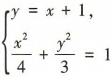 得7x2+8x-8=0,解得
得7x2+8x-8=0,解得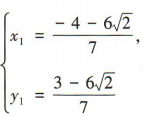 或
或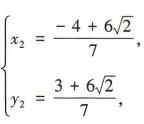 所以 △OMN的面积
所以 △OMN的面积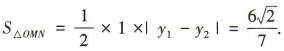
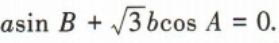 (1)求角A的大小;
(2)若b=4,△ABC的面积
(1)求角A的大小;
(2)若b=4,△ABC的面积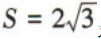 求△ABC的周长.
求△ABC的周长.