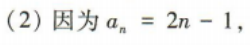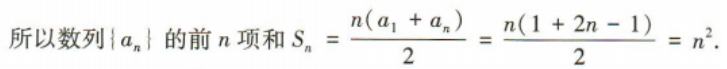2024年高职单招《数学(中职)》每日一练试题10月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知集合M={3,4,5},则M的非空子集有()
答 案:C
解 析:∵集合M={3,4,5},∴M的非空子集有23-1=7(个).
2、在同一直角坐标系中,指数函数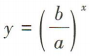 和二次函数y=ax²-bx的大致图象可能是()
和二次函数y=ax²-bx的大致图象可能是()
答 案:B
解 析:若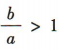 ,则函数
,则函数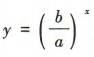 是增函数,当a<0时,函数
是增函数,当a<0时,函数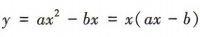 的图象开口向下,与x轴的交点分别为
的图象开口向下,与x轴的交点分别为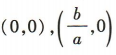 ,故选项A不正确,选项B正确.若
,故选项A不正确,选项B正确.若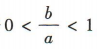 ,则函数
,则函数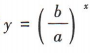 是减函数,当a>0时,函数
是减函数,当a>0时,函数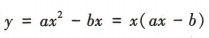 的图象开口向上,与x轴的交点分别为
的图象开口向上,与x轴的交点分别为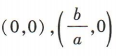 ,故选项C,D都不正确。
,故选项C,D都不正确。
3、
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:A
解 析:由2x<2得x<1,所以“-2x<2”的充分不必要条件
4、将图中所示的直角梯形ABCD绕AB所在的直线旋转一周,由此形成的几何体的体积是() 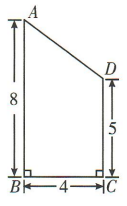
答 案:C
解 析:将题图中的直角梯形ABCD绕AB所在直线旋转一周可得上部分为圆锥,下部分为圆柱的组合体.易知圆锥的底面半径为4,高为3,圆柱的底面半径为4,高为5,所以该组合体的体积为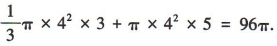
填空题
1、不等式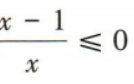 的解集为()
的解集为()
答 案:(0,1]
解 析:
2、过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线的方程为()
答 案:2x+y-8=0
解 析:由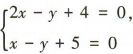 得
得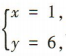 所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
3、设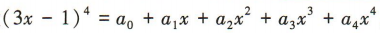 ,则
,则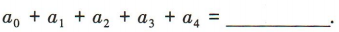
答 案:16
解 析:令x=1,得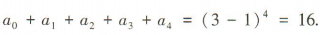
4、(2+x)6展开式中含x3项的二项式系数为()
答 案:20
解 析:(2+x)6展开式中含x3项的二项式系数为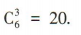
简答题
1、某物业管理公司有75套公寓对外出租,经市场调查发现,每套公寓租价为2500元时,可以全部租出,租价每上涨100元就会少租出一套公寓,问:每套公寓租价为多少元时,租金总收入最大?最大收入为多少元?
答 案:设每套公寓租价上涨100x元,则每套公寓的租价为(2500+100x)元,共租出(75-x)套. 依题意,租金总收入y=(2500+100x)(75-x)=-100x2+5000x+187500=-100(x-25)2+250000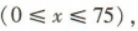 则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
2、已知数列{an}中,a1=1,an=2n-1.
(1)证明{an}是等差数列;
(2)求数列{an}的前n项和Sn.
答 案:(1)因为an+1-an=[2(n+1)-1]-(2n-1)=2,a1=1, 所以数列{an}是以1为首项,2为公差的等差数列.
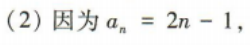
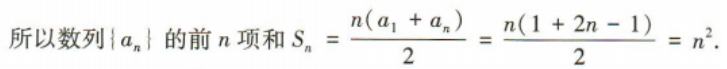
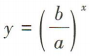 和二次函数y=ax²-bx的大致图象可能是()
和二次函数y=ax²-bx的大致图象可能是()
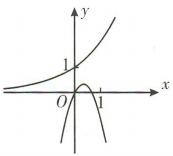
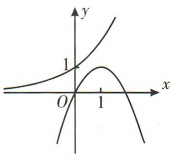
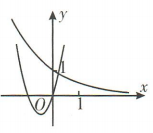
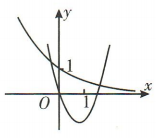
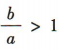 ,则函数
,则函数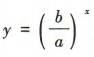 是增函数,当a<0时,函数
是增函数,当a<0时,函数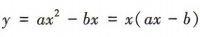 的图象开口向下,与x轴的交点分别为
的图象开口向下,与x轴的交点分别为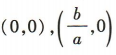 ,故选项A不正确,选项B正确.若
,故选项A不正确,选项B正确.若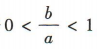 ,则函数
,则函数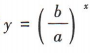 是减函数,当a>0时,函数
是减函数,当a>0时,函数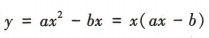 的图象开口向上,与x轴的交点分别为
的图象开口向上,与x轴的交点分别为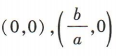 ,故选项C,D都不正确。
,故选项C,D都不正确。

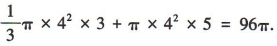
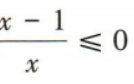 的解集为()
的解集为()
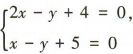 得
得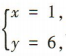 所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.
所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.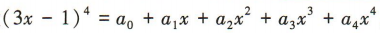 ,则
,则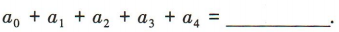
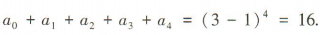
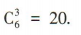
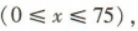 则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.