2024年高职单招《数学(中职)》每日一练试题10月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知i是虚数单位,则(2-i)i=()
- A:1-2i
- B:1 + 2i
- C:-1-2i
- D:-1+2i
答 案:B
解 析:(2-i)i = 2i-i2=1 + 2i.
2、从 1,2,3,4,5中任选3个数,从7,8,9中任选2个数,可组成无重复数字的五位数的个数为()
答 案:B
解 析:先从1,2,3,4,5中任选3个数,方法有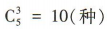 ;再从7,8,9中任取2个数字,方法有
;再从7,8,9中任取2个数字,方法有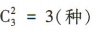 ;最后把这5个数组成无重复数字的五位数,方法有
;最后把这5个数组成无重复数字的五位数,方法有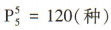 .根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.
.根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.
3、已知A(-1,-1),B(1,3),C(x,5),若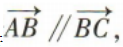 则x=()
则x=()
答 案:A
解 析:
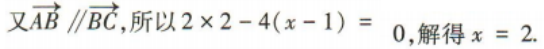
4、已知函数f(x)=x²-2x+3的最小值为()
答 案:D
解 析:易知函数f(x)=x²-2x+3的图象开口向上,对称轴为直线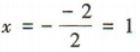 所以f(x)的最小值为f(1)=2.
所以f(x)的最小值为f(1)=2.
填空题
1、若10件产品中有2件次品,现从中任取3件,则至少有一件是次品的取法共有()种。
答 案:64
解 析:从 10件产品中任取3件的取法共有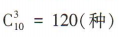 ,其中一件次品都没有的取法共有
,其中一件次品都没有的取法共有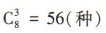 ,所以至少有一件次品的取法共有120-56=64(种).
,所以至少有一件次品的取法共有120-56=64(种).
2、已知等差数列{an}的公差是正数,且 a3a7=-12,a4+ a6=-4,则a20=()
答 案:28
解 析: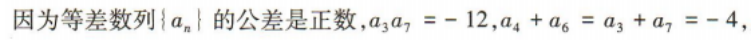
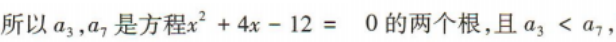

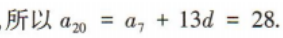
3、已知方程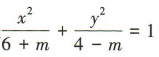 表示焦点在y轴上的椭圆,则实数m的取值范围是()
表示焦点在y轴上的椭圆,则实数m的取值范围是()
答 案:(-6,-1)
解 析:因为方程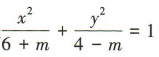 表示焦点在y轴上的椭圆,所以
表示焦点在y轴上的椭圆,所以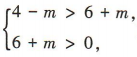 解得 -6
解得 -6
4、某班有学生60人,将这60名学生随机编号为1~60号,用系统抽样的方法从中抽出4名学生,已知2号,32号,47号学生在样本中,则样本中另一个学生的编号为()
答 案:17
解 析:由题意知分段间隔为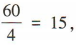 则样本中另一个学生的编号为 17.
则样本中另一个学生的编号为 17.
简答题
1、已知椭圆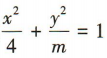 与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为
与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为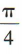 的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
(2)求△OMN的面积(O为坐标原点)
答 案:(1)易得抛物线y2= 4x的焦点为F2(1,0), 所以椭圆的左焦点为F1(-1,0).
又直线 MN 的斜率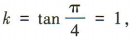 所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为
所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为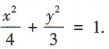 (2)设M,N的坐标分别为(x1,y1),(x2,y2).
由
(2)设M,N的坐标分别为(x1,y1),(x2,y2).
由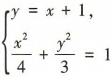 得7x2+8x-8=0,解得
得7x2+8x-8=0,解得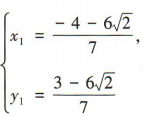 或
或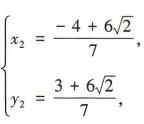 所以 △OMN的面积
所以 △OMN的面积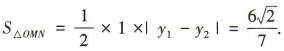
2、如图,在四棱锥P-ABCD中,底面四边形 ABCD为菱形,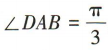 ,
,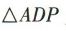 为等边三角形.
(1)证明
为等边三角形.
(1)证明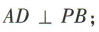 (2)若AB=2,BP=
(2)若AB=2,BP=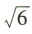 ,求直线 PB 与平面 ABCD 所成的角,
,求直线 PB 与平面 ABCD 所成的角,
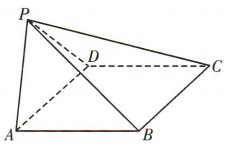
答 案:(1)连接 BD. 因为四边形 ABCD为菱形,且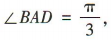 所以 △ADB 为等边三角形.
取线段AD的中点E,连接BE,PE,则
所以 △ADB 为等边三角形.
取线段AD的中点E,连接BE,PE,则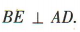 又 △PAD 为等边三角形,
所以
又 △PAD 为等边三角形,
所以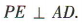 因为
因为 所以
所以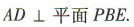 又
又 所以
所以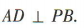 (2)由AB=2可得
(2)由AB=2可得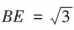 ,AD=2,则
,AD=2,则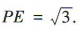 又
又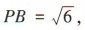 所以
所以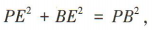 所以
所以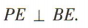 又
又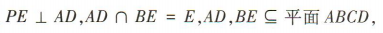 所以
所以 所以
所以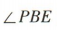 为直线PB与平面ABCD所成的角,
为直线PB与平面ABCD所成的角,
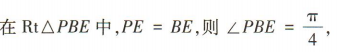 所以直线PB与平面ABCD 所成的角为
所以直线PB与平面ABCD 所成的角为
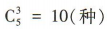 ;再从7,8,9中任取2个数字,方法有
;再从7,8,9中任取2个数字,方法有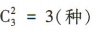 ;最后把这5个数组成无重复数字的五位数,方法有
;最后把这5个数组成无重复数字的五位数,方法有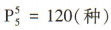 .根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.
.根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.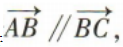 则x=()
则x=()
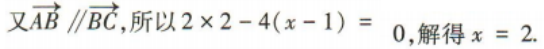
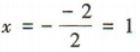 所以f(x)的最小值为f(1)=2.
所以f(x)的最小值为f(1)=2.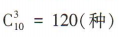 ,其中一件次品都没有的取法共有
,其中一件次品都没有的取法共有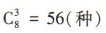 ,所以至少有一件次品的取法共有120-56=64(种).
,所以至少有一件次品的取法共有120-56=64(种).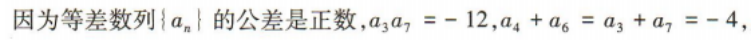
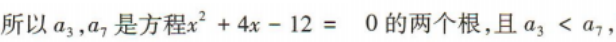

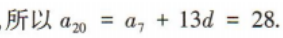
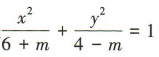 表示焦点在y轴上的椭圆,则实数m的取值范围是()
表示焦点在y轴上的椭圆,则实数m的取值范围是()
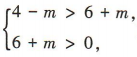 解得 -6
解得 -6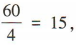 则样本中另一个学生的编号为 17.
则样本中另一个学生的编号为 17.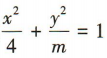 与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为
与抛物线y2=4x有共同的焦点F2,过椭圆的左焦点F1作倾斜角为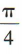 的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;
的直线,与椭圆相交于 M,N两点.(1)求直线 MN 的方程和椭圆的方程;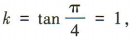 所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为
所以直线 MN的方程为y=x+1,即x-y+1=0.
由题意知椭圆焦点在x轴上,且c=1,
所以m=4-1=3,
所以椭圆的方程为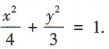 (2)设M,N的坐标分别为(x1,y1),(x2,y2).
由
(2)设M,N的坐标分别为(x1,y1),(x2,y2).
由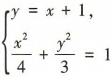 得7x2+8x-8=0,解得
得7x2+8x-8=0,解得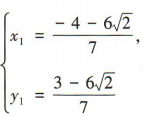 或
或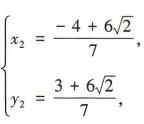 所以 △OMN的面积
所以 △OMN的面积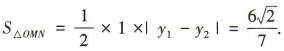
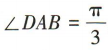 ,
,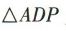 为等边三角形.
(1)证明
为等边三角形.
(1)证明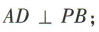 (2)若AB=2,BP=
(2)若AB=2,BP=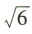 ,求直线 PB 与平面 ABCD 所成的角,
,求直线 PB 与平面 ABCD 所成的角,

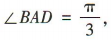 所以 △ADB 为等边三角形.
取线段AD的中点E,连接BE,PE,则
所以 △ADB 为等边三角形.
取线段AD的中点E,连接BE,PE,则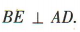 又 △PAD 为等边三角形,
所以
又 △PAD 为等边三角形,
所以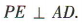 因为
因为 所以
所以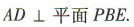 又
又 所以
所以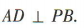 (2)由AB=2可得
(2)由AB=2可得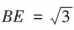 ,AD=2,则
,AD=2,则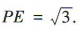 又
又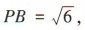 所以
所以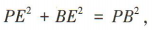 所以
所以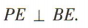 又
又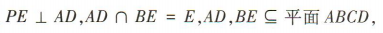 所以
所以 所以
所以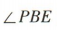 为直线PB与平面ABCD所成的角,
为直线PB与平面ABCD所成的角,
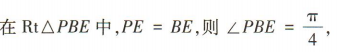 所以直线PB与平面ABCD 所成的角为
所以直线PB与平面ABCD 所成的角为



