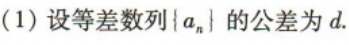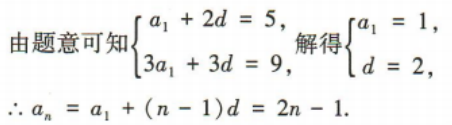2024年高职单招《数学(中职)》每日一练试题10月19日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知Sn为等差数列{an}的前n项和,a₁=5,公差d=2,若Sm=140,则m=()
答 案:D
解 析:由题意得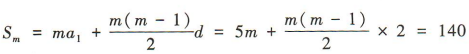 ,即m²+4m-140=0,解得m=10,m=-14(舍去).
,即m²+4m-140=0,解得m=10,m=-14(舍去).
2、已知某圆锥的侧面展开图为半圆,该圆锥的体积为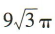 ,则该圆锥的表面积为
,则该圆锥的表面积为
- A:27π
- B:
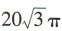
- C:

- D:16π
答 案:A
解 析:设圆锥底面的半径为r,母线长为l,由题意得2πr= πl,所以l= 2r,所以圆锥的高为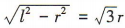 ,所以圆锥的体积为
,所以圆锥的体积为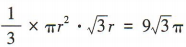 ,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.
,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.
3、现有甲、乙两组样本数据,甲组的数据为1,3,3,3,5,乙组的数据为1,2,3,4,5,设甲组数据的平均数为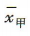 ,乙组数据的平均数为
,乙组数据的平均数为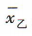 ,两组数据的标准差分别为
,两组数据的标准差分别为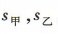 ,则()
,则()
答 案:A
解 析:易知甲组数据的平均数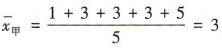 ,乙组数据的平均数
,乙组数据的平均数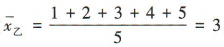 ,则甲组数据的标准差
,则甲组数据的标准差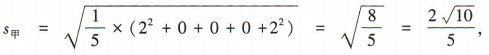 乙组数据的标准差
乙组数据的标准差
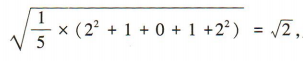 所以
所以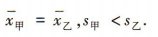
4、
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:A
解 析:由2x<2得x<1,所以“-2x<2”的充分不必要条件
填空题
1、数列x,2,y既是等差数列又是等比数列,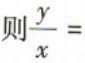 ()
()
答 案:1
解 析:
2、双曲线 25x2-16y2=400 的渐近线方程为()
答 案:5x±4y =0
解 析:将双曲线方程25x2-16y2=400化为标准方程为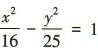 ,所以双曲线25x2-16y2=400的渐近线方程为5x±4y=0.
,所以双曲线25x2-16y2=400的渐近线方程为5x±4y=0.
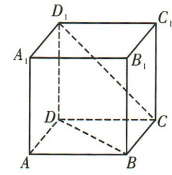
3、如图,在正方体ABCD-A1B1C1D1中,异面直线D1C与BD 所成角的大小为()
答 案:60°
解 析:在正方体ABCD-A1B1C1D1中,连接B1D1与B1C,如图.易得BD//B1D1,所以 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知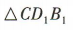 是正三角形,所以
是正三角形,所以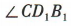 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 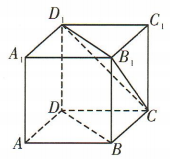
4、如图,画一个边长为4的正方形,再将这个正方形各边的中点相连得到第2个正方形,依此类推,这样一共画了10个正方形,则第10个正方形的面积为()

答 案: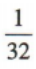
解 析:由题意知,第一个正方形的边长a1=4,面积T1=16;第二个正方形的边长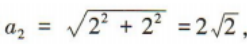 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长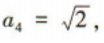 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
简答题
1、已知集合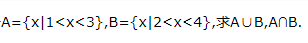
答 案: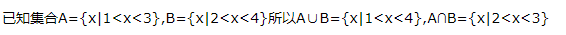
2、记等差数列{an}的前n项和为Sn,a3=5,S3=9
(1)求数列{an}的通项公式;
(2)记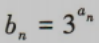 求数列{bn}的前n项和Tn.
求数列{bn}的前n项和Tn.
答 案: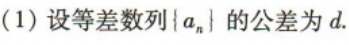
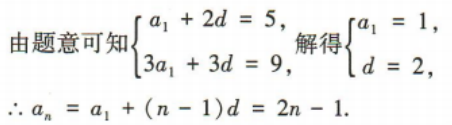

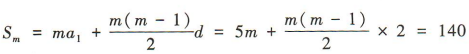 ,即m²+4m-140=0,解得m=10,m=-14(舍去).
,即m²+4m-140=0,解得m=10,m=-14(舍去).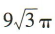 ,则该圆锥的表面积为
,则该圆锥的表面积为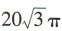

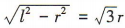 ,所以圆锥的体积为
,所以圆锥的体积为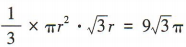 ,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.
,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.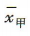 ,乙组数据的平均数为
,乙组数据的平均数为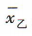 ,两组数据的标准差分别为
,两组数据的标准差分别为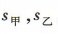 ,则()
,则()
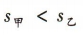
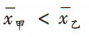
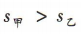
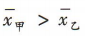
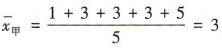 ,乙组数据的平均数
,乙组数据的平均数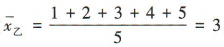 ,则甲组数据的标准差
,则甲组数据的标准差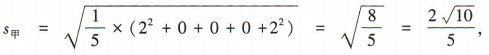 乙组数据的标准差
乙组数据的标准差
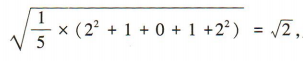 所以
所以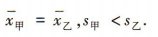

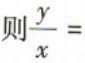 ()
()
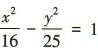 ,所以双曲线25x2-16y2=400的渐近线方程为5x±4y=0.
,所以双曲线25x2-16y2=400的渐近线方程为5x±4y=0.
 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知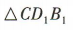 是正三角形,所以
是正三角形,所以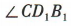 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 

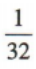
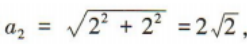 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长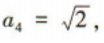 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
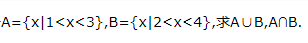
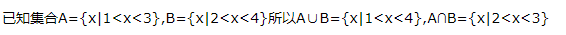
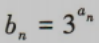 求数列{bn}的前n项和Tn.
求数列{bn}的前n项和Tn.