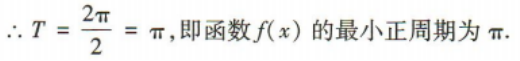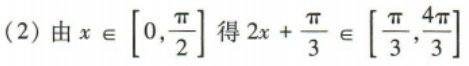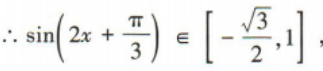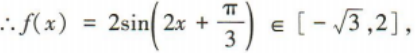2024年高职单招《数学(中职)》每日一练试题10月17日

2024年高职单招《数学(中职)》每日一练试题10月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知两个单位向量a,b的夹角是120°,则|a-b|=()  

• A：1
• B：
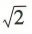
• C：2
• D：

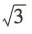
答 案：D

解 析：因为两个单位向量a,b的夹角是120°,所以

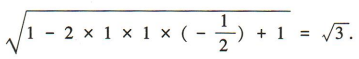
2、函数f(x)=x|x|的图像（）

• A：关于原点对称
• B：关于x轴对称
• C：关于y轴对称
• D：关于y=x对称

答 案：A

解 析：由f(-x)=-x|-x|=-x|x|=-f(x),且函数f(x)的定义域为R可知f(x)是奇函数，其图像关于原点对称.

3、的()

• A：充分条件
• B：必要条件
• C：充要条件
• D：既不充分也不必要条件

答 案：A

解 析：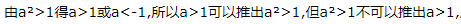

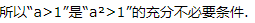
4、已知函数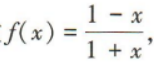且f(a)=3,则a的值为()

• A：
• B：
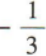
• C：
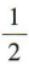
• D：

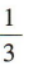
答 案：A

解 析：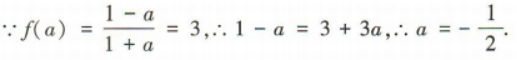

填空题

1、已知以 F₁,F₂为焦点的椭圆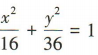交x轴正半轴于点4,则△AF₁F₂的面积为()  

答 案：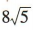

解 析：由题意得a²= 36,b²= 16,所以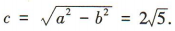因为椭圆与x轴正半轴交于点A,所以A(4,0),所以

2、不等式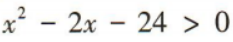的解集为（）  

答 案：(-∞,-4)U(6,+∞)

解 析：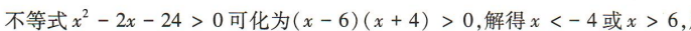

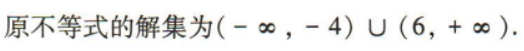
3、从1,2,3,4这些数字中任取两个不同的数,则可以组成不同的两位数的个数为（）  

答 案：12

解 析：从1,2,3,4这四个数字中任取两个不同的数,可以组成不同的两位数的个数为

4、已知等差数列{a_n}的前n项和为S_n,且S₂=4,S₄=16,则 a₅+a₆=（）  

答 案：20

解 析：∵{an}为等差数列，前n项和为S_n,∴S₂,S₄-S₂,S₆-S₄成等差数列，∴2(S₄-S₂)=S₂+(S₆-S₄),又S₂=4,S₄=16,∴24=4+S₆-S₄=a₅+a₆+4,∴a₅+a₆=20.

简答题

1、如图,四边形 ABCD是矩形,,,且AB=1,AD =MA = 2. 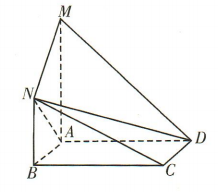(1)证明:NC//平面MAD.
(2)求三棱锥M-NAD 的体积.  

答 案：(1)∵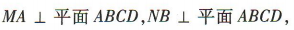 ∴MA // NB. 又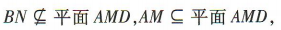 ∴BN//平面AMD. ∵四边形 ABCD 是矩形， ∴BC//AD. 又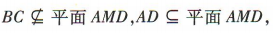 ∴BC//平面AMD. ∵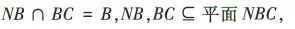 ∴平面NBC//平面MAD. ∵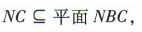 ∴NC //平面MAD. (2)易知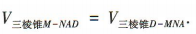 在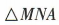中,易得边MA上的高h=AB=1, ∴ ∴  

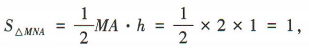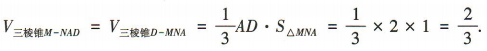
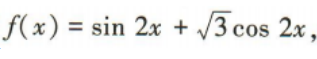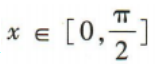2、已知函数x∈R. (1)求函数f(x)的最小正周期； (2)求函数f(x)在上的最值.

答 案：