2024年高职单招《数学(中职)》每日一练试题10月16日

2024年高职单招《数学(中职)》每日一练试题10月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若α为钝角，且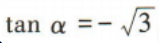,则α=（）

• A：30°
• B：60°
• C：120°
• D：150°

答 案：C

解 析：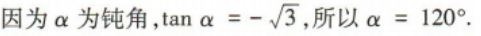

2、函数f(x)=√3sinx-cosx的值域为（）

• A：[-√3,√3]
• B：[-√3-1,√3+1]
• C：[-1,1]
• D：[-2,2]

答 案：D

解 析：易知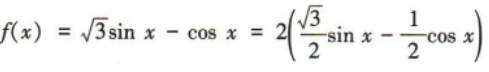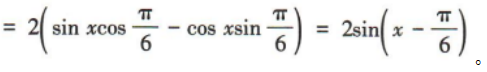。因为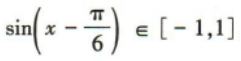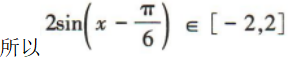，所以函数f(x)=√3sinx-cosx的值域为[-2,2].

3、如图,直线a//平面α,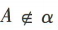,且直线a与点A位于α的两侧,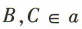,AB,AC分别交平面α于点E,F.若BC=4.CF=5,AF=3,则EF的长为()  

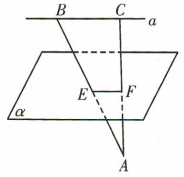
• F：若BC=4.CF=5,AF=3,则EF的长为()
• A：3
• B：
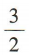
• C：
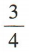
• D：

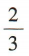
答 案：B

解 析：

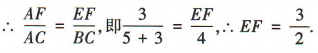
4、已知直线l₁:mx+y+3=0,l₂:2x-y+3=0.若l₁⊥l₂,则m=()  

• A：
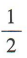
• B：
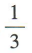
• C：2
• D：3

答 案：A

解 析：因为直线l₁:mx+y+3=0与直线l₂:2x-y+3=0垂直，所以2m-1=0,解得

填空题

1、某校有 900名学生,其中女生 400名.按男女比例用分层抽样的方法,从该校学生中抽取一个容量为45 的样本,则应抽取男生的人数为()  

答 案：25

解 析：应抽取男生的人数为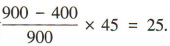

2、已知等差数列{a_n}的前n项和S_n=4n²-n,则公差d=（）

答 案：8

解 析：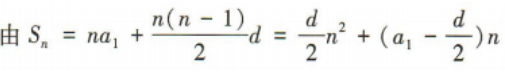

3、如图,在正方体ABCD-A₁B₁C₁D₁中,异面直线D₁C与BD 所成角的大小为()  

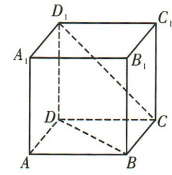
答 案：60°

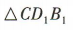解 析：在正方体ABCD-A₁B₁C₁D₁中,连接B₁D₁与B₁C,如图.易得BD//B₁D₁,所以为异面直线D₁C与BD所成的角.易知是正三角形,所以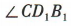=60°,所以异面直线 D₁C与 BD 所成角的大小为 60°.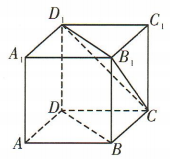  

4、不等式的解集为（）(用区间表示)

答 案：(-1,0)∪(0,+∞)

解 析：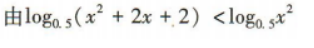

简答题

1、已知a,b,c分别为△ABC的内角A,B,C的对边，且c²=2ab. (1)若C=90°,且a=1,求△ABC的面积； (2)若sinA=sinC,求cosC的值.

答 案：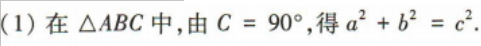

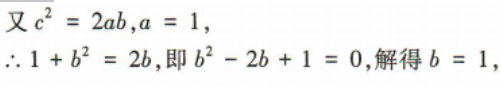
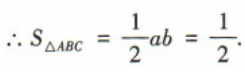
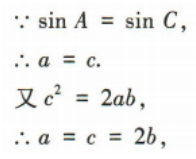
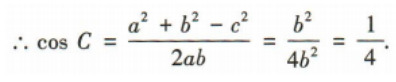
2、制作一个高为20cm的长方体容器，底面矩形的长比宽长10cm,并且容积不少于4000cm³,问底面矩形的宽至少应是多少?

答 案：设底面矩形的宽为x cm. 由题意可得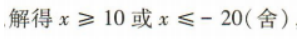所以底面矩形的宽至少为10cm.