2024年高职单招《数学(中职)》每日一练试题10月14日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、直线3x-y-1=0的斜率k及在y轴上的截距b分别是()
- A:k=3,b=-1
- B:k=-3,b=1
- C:
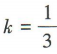 ,b=1
,b=1 - D:k=3,b=1
答 案:A
解 析:由直线3x-y-1=0得y=3x-1,所以直线的斜率k=3,在y轴上的截距b=-1.
2、已知抛物线的顶点在坐标原点,准线方程为y=4,则该抛物线的方程为()
- A:y²=16x
- B:y²=-16x
- C:x²=16y
- D:x²=-16y
答 案:D
解 析:易知抛物线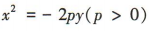 的准线方程为
的准线方程为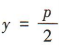 ,所以准线方程为y=4的抛物线方程为x²=-16y.
,所以准线方程为y=4的抛物线方程为x²=-16y.
3、在x∈[0,2π]上,满足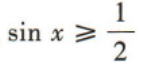 的x的取值范围是()
的x的取值范围是()
答 案:B
解 析: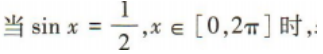

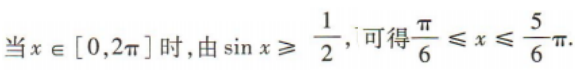
4、若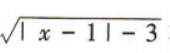 有意义,则x的取值范围是()
有意义,则x的取值范围是()
- A:(-2,4)
- B:(-∞,-2)∪(4,+∞)
- C:[-2,4]
- D:(-∞,-2]∞[4,+∞)
答 案:D
解 析:
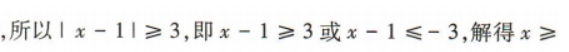

填空题
1、若抛物线y=ax2-6x+c的开口向下,且与y轴交于正半轴,则抛物线的顶点位于第()象限.
答 案:二
解 析:因为抛物线y=ax2-6x+c的开口向下,且与y轴交于正半轴,
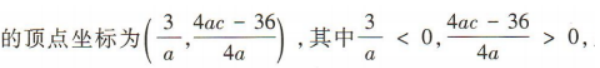 所以抛物线的顶点位于第二象限
所以抛物线的顶点位于第二象限
2、满足M∪{1}={0.1.2}的集合M的个数为()
答 案:2
解 析:因为M∪{1}={0,1,2},所以0,2必须是集合M中的元素,1可以是集合M中的元素,也可以不是集合M中的元素,所以M={0,2}或M={0,1,2},所以满足题意的M的个数是2.
3、已知集合A={1.2},B={a,1},若A∪B={1.2.3}.则实数a的值为()
答 案:3
解 析:由题可知A={1,2},B={a,1},且A∪B={1,2,3},所以a=3.
4、已知抛物线的方程为y2=8x,则抛物线的焦点到准线的距离是()
答 案:4
解 析:因为抛物线的方程为y2=2px=8x,所以抛物线的焦点到准线的距离p=4.
简答题
1、如图,在底面是矩形的四棱锥P-ABCD中, ,E,F分别是 PC,PD的中点. (1)若PA=AB=1.BC=2.求四棱锥P-ABCD的体积; (2)证明
,E,F分别是 PC,PD的中点. (1)若PA=AB=1.BC=2.求四棱锥P-ABCD的体积; (2)证明
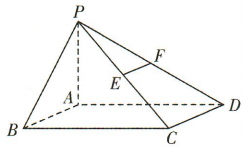
答 案:(1) ∴PA为四棱锥P-ABCD的高.
又PA=AB=1,BC=2,底面ABCD 是矩形,
∴
∴PA为四棱锥P-ABCD的高.
又PA=AB=1,BC=2,底面ABCD 是矩形,
∴ (2)∵四边形 ABCD 为矩形,
∴
(2)∵四边形 ABCD 为矩形,
∴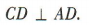 ∵
∵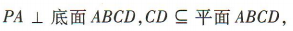 ∴
∴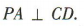 又
又 ∴
∴ 又E,F分别是 PC,PD的中点,
∴ EF // CD,
∴
又E,F分别是 PC,PD的中点,
∴ EF // CD,
∴
2、甲、乙两人独立地破译一份密码,已知甲、乙两人各自能破译的概率分别是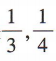 ,求:(1)甲、乙两人都成功破译密码的概率;
,求:(1)甲、乙两人都成功破译密码的概率;
(2)密码被成功破译的概率.
答 案:记“甲译出密码”的事件为 A,“乙译出密码”的事件为 B,“密码被成功破译”的事件为C, 则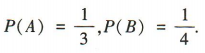 (1)由题意得P(AB)= P(4)·P(B)=
(1)由题意得P(AB)= P(4)·P(B)=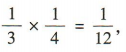 所以两人都成功破译的概率为
所以两人都成功破译的概率为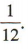 (2)易得事件A的对立事件的概率
(2)易得事件A的对立事件的概率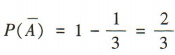 ,事件B的对立事件的概率
,事件B的对立事件的概率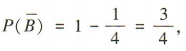 所以甲乙两人都没有成功破译密码的概率
所以甲乙两人都没有成功破译密码的概率 所以
所以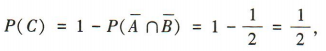 所以密码被成功破译的概率为
所以密码被成功破译的概率为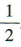
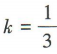 ,b=1
,b=1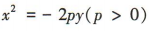 的准线方程为
的准线方程为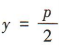 ,所以准线方程为y=4的抛物线方程为x²=-16y.
,所以准线方程为y=4的抛物线方程为x²=-16y.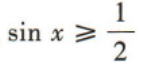 的x的取值范围是()
的x的取值范围是()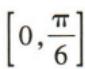
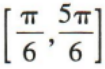
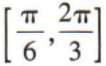
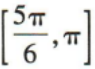
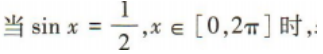

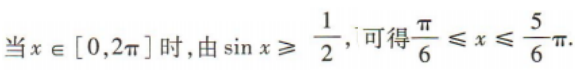
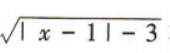 有意义,则x的取值范围是()
有意义,则x的取值范围是()
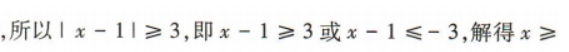


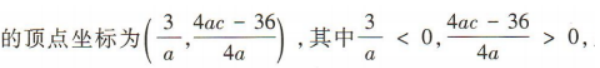 所以抛物线的顶点位于第二象限
所以抛物线的顶点位于第二象限 ,E,F分别是 PC,PD的中点. (1)若PA=AB=1.BC=2.求四棱锥P-ABCD的体积; (2)证明
,E,F分别是 PC,PD的中点. (1)若PA=AB=1.BC=2.求四棱锥P-ABCD的体积; (2)证明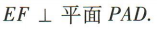

 ∴PA为四棱锥P-ABCD的高.
又PA=AB=1,BC=2,底面ABCD 是矩形,
∴
∴PA为四棱锥P-ABCD的高.
又PA=AB=1,BC=2,底面ABCD 是矩形,
∴ (2)∵四边形 ABCD 为矩形,
∴
(2)∵四边形 ABCD 为矩形,
∴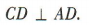 ∵
∵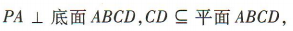 ∴
∴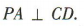 又
又 ∴
∴ 又E,F分别是 PC,PD的中点,
∴ EF // CD,
∴
又E,F分别是 PC,PD的中点,
∴ EF // CD,
∴
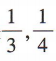 ,求:(1)甲、乙两人都成功破译密码的概率;
,求:(1)甲、乙两人都成功破译密码的概率;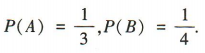 (1)由题意得P(AB)= P(4)·P(B)=
(1)由题意得P(AB)= P(4)·P(B)=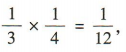 所以两人都成功破译的概率为
所以两人都成功破译的概率为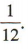 (2)易得事件A的对立事件的概率
(2)易得事件A的对立事件的概率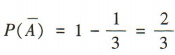 ,事件B的对立事件的概率
,事件B的对立事件的概率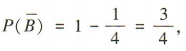 所以甲乙两人都没有成功破译密码的概率
所以甲乙两人都没有成功破译密码的概率 所以
所以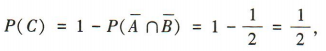 所以密码被成功破译的概率为
所以密码被成功破译的概率为