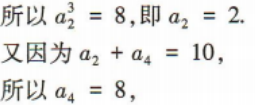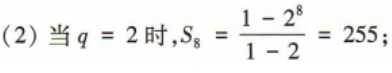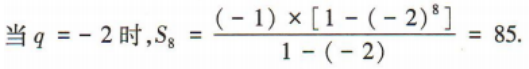2024年高职单招《数学(中职)》每日一练试题10月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
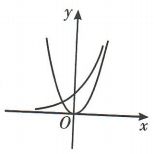
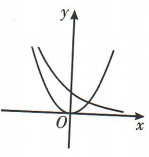
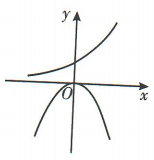
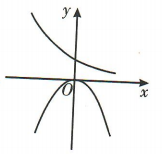
1、当a>1时,函数y=ax和y=(a-1)x²的图象只可能是()
答 案:A
解 析:当a>1时,指数函数y=ax为增函数,二次函数y=(a-1)x2的图象开口向上,且函数y=(a-1)x2图象的对称轴为y轴,因此函数y=ax和y=(a-1)x2的图象只可能是A选项中的图象.
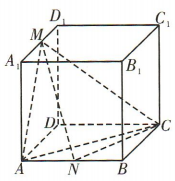
2、如图,已知正方体 ABCD-A1B1C1D1的体积为1,M,N分别是棱A1D1,AB 的中点,则三棱锥M-ANC的体积为()
答 案:D
解 析:易知正方体 ABCD - A1B1C1D1的棱长为1.由题意知三棱锥 M-ANC的高为1,底面三角形 ANC的面积为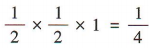 ,所以三棱锥M-ANC的体积
,所以三棱锥M-ANC的体积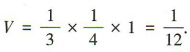
3、设函数f(x)=ax+bx3+2 023,且f(-2)=5,则f(2)=()
- A:-5
- B:-2 018
- C:20 28
- D:4 041
答 案:D
解 析:令g(x)=ax+bx3,则g(x)是奇函数,且g(x)=f(x)-2 023,所以g(-2)=f(-2)-2 023=-2 018,所以g(2)=-g(-2)=2 018=f(2)-2 023,所以f(2)=4 041.
4、某地为了保护水土资源,实施山林绿化工程,如果2023年绿化面积是8万公顷,以后每年的绿化面积都比上一年多1万公顷,那么2026年的绿化面积是()
- A:9万公顷
- B:10万公顷
- C:11万公顷
- D:12万公顷
答 案:C
解 析:因为2023年该地的绿化面积是8万公顷,以后每年的绿化面积都比上一年多1万公顷,所以2026年该地的绿化面积是8+3=11(万公顷).
填空题
1、若向量a与b共线,且|a|=|b|=1,则|a+b|=()
答 案:0或2
解 析:∵向量a与b共线,且|a|=|b|,∴a与b相等或互为相反向量.当a与b相等时,|a+b|=|2a|=2;当a与b互为相反向量时,|a+b|=|0|=0.
2、已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)=()
答 案:
解 析: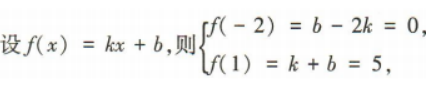

3、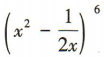 展开式中的常数项为()
展开式中的常数项为()
答 案: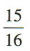
解 析:易知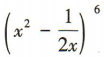 展开式的通项为
展开式的通项为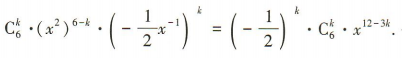 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以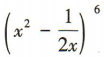 展开式中的常数项为
展开式中的常数项为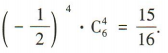
4、若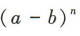 的二项展开式中系数最大的项只有第7项,则n的值为()
的二项展开式中系数最大的项只有第7项,则n的值为()
答 案:12
解 析:易知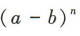 的二项展开式有n+1项.因为
的二项展开式有n+1项.因为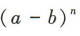 的二项展开式中系数最大的项只有第7项,所以n+1 = 13.解得 n = 12.
的二项展开式中系数最大的项只有第7项,所以n+1 = 13.解得 n = 12.
简答题
1、某网店销售一批新款削笔器,每个削笔器的最低售价为15元.若按最低售价销售,每天能卖出30个;若一个削笔器的售价每提高1元,日销售量将减少2个.该店店长为了每天获得400元以上的销售收入,应怎样制定这批削笔器的销售价格?
答 案:设这批削笔器的销售价格定为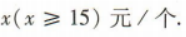 由题意得
由题意得
 故这批削笔器的销售价格在每个15元到20元之间(包括15元但不包括20元),才能每天获得400元以上的销售收入.
故这批削笔器的销售价格在每个15元到20元之间(包括15元但不包括20元),才能每天获得400元以上的销售收入.
2、在等比数列{an}中,a1a2a3=8,a2+a4=10. (1)求首项a1及公比q; (2)求该数列的前8项和S8
答 案:
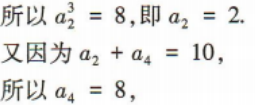

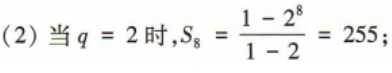
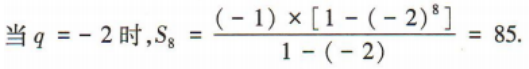

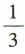
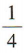
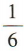
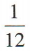
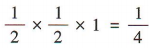 ,所以三棱锥M-ANC的体积
,所以三棱锥M-ANC的体积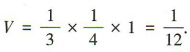

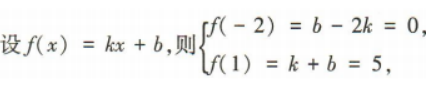

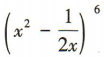 展开式中的常数项为()
展开式中的常数项为()
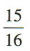
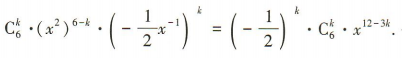 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以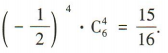
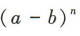 的二项展开式中系数最大的项只有第7项,则n的值为()
的二项展开式中系数最大的项只有第7项,则n的值为() 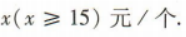 由题意得
由题意得
 故这批削笔器的销售价格在每个15元到20元之间(包括15元但不包括20元),才能每天获得400元以上的销售收入.
故这批削笔器的销售价格在每个15元到20元之间(包括15元但不包括20元),才能每天获得400元以上的销售收入.