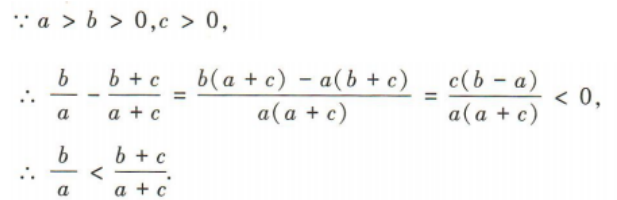2024年高职单招《数学(中职)》每日一练试题10月08日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知等比数列{an}的公比为q,前n项和为Sn.若q=2,S1=-2,则S4=()
答 案:C
解 析:
2、若a∈R,则“a²=1”是“a=1”的()
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:B
解 析:由a2=1,得a=±1,所以由“a2=1”不能推出“a=1”.由“a=1”能推出“a2=1”,所以“a2=1”是“a=1”的必要不充分条件
3、某公司有五个不同部门,现有4名在校大学生来该公司实习,要求安排到该公司的两个部门,且每个部门安排两名,则不同的安排方案种数为()
答 案:A
解 析:先将4名大学生分为人数分别为2,2的两组,则分组方案有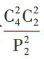 种;再将此两组大学生分到五个部门中的两个部门中,不同的安排方式有
种;再将此两组大学生分到五个部门中的两个部门中,不同的安排方式有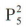 种,故不同的安排方案有
种,故不同的安排方案有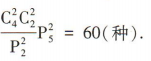
4、下列结论正确的是()
- A:若ac>bc,则a>b
- B:若a²>b²,则a>b
- C:若a>b,c<0,则ac<bc
- D:若
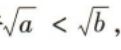 ,则a>b
,则a>b
答 案:C
解 析:若a=-2,b=-1,c=-1,满足ac>bc,但a<b,所以A错误;当a<b<0时,满足a²>b²,但a<b,所以B错误;若a>b,c<0,则ac<bc,所以C正确;若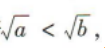 则a<b,所以D错误.
则a<b,所以D错误.
填空题
1、函数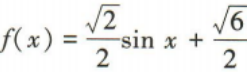 的最小值为
的最小值为
答 案: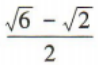
解 析: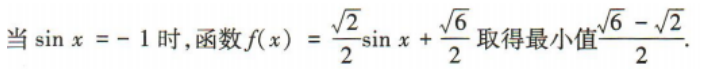
2、已知 那么sin(π+α)=()
那么sin(π+α)=()
答 案: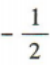
解 析: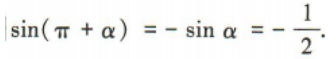
3、直线2x+3y+6=0在y轴上的截距是()
答 案:-2
解 析:由2x+3y+6=0,得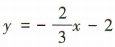 ,所以直线2x+3y+6=0在y轴上的截距为 - 2.
,所以直线2x+3y+6=0在y轴上的截距为 - 2.
4、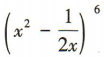 展开式中的常数项为()
展开式中的常数项为()
答 案: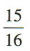
解 析:易知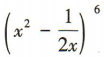 展开式的通项为
展开式的通项为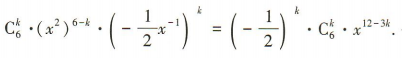 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以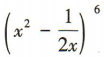 展开式中的常数项为
展开式中的常数项为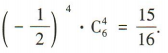
简答题
1、已知 判断
判断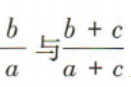 大小关系.
大小关系.
答 案: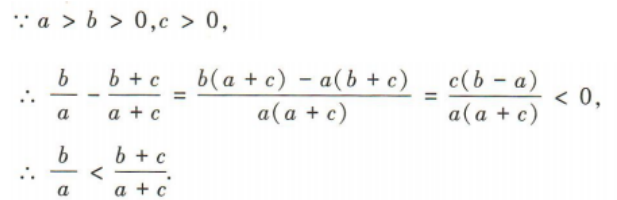
2、已知函数f(x)=(x-m)2+2.
(1)若函数f(x)的图像过点(2,2),求函数y=f(x)的单调递增区间;
(2)若函数f(x)是偶函数,求m的值
答 案:(1)由题意知f(2)=(2-m)2+2=2, ∴.m=2,即f(x)=(x-2)2+2,
∴函数f(x)的单调递增区间为[2,+∞).
(2)∵函数f(x)是偶函数,
∴.f(-x)=f(x),即(-x-m)2+2=(x-m)2+2,
∴m=0.

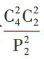 种;再将此两组大学生分到五个部门中的两个部门中,不同的安排方式有
种;再将此两组大学生分到五个部门中的两个部门中,不同的安排方式有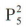 种,故不同的安排方案有
种,故不同的安排方案有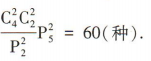
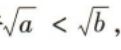 ,则a>b
,则a>b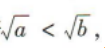 则a<b,所以D错误.
则a<b,所以D错误.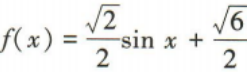 的最小值为
的最小值为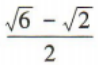
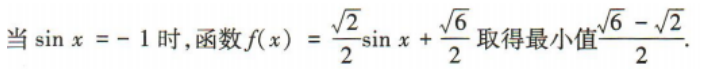
 那么sin(π+α)=()
那么sin(π+α)=()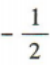
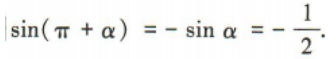
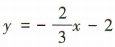 ,所以直线2x+3y+6=0在y轴上的截距为 - 2.
,所以直线2x+3y+6=0在y轴上的截距为 - 2.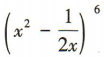 展开式中的常数项为()
展开式中的常数项为()
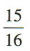
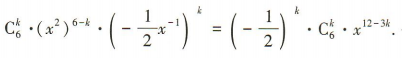 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以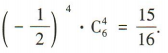
 判断
判断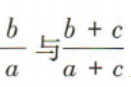 大小关系.
大小关系.