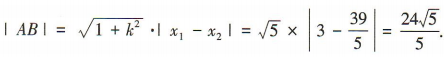2024年高职单招《数学(中职)》每日一练试题10月03日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、“x为有理数”是“x2为有理数”的()
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:A
解 析:x为有理数,则x2一定为有理数,但x2为有理数,x不一定为有理数,比如3为有理数,但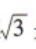 是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
2、圆(x-4)²+y²=4的圆心到直线x-y+4=0的距离为()
答 案:D
解 析:易知圆(x-4)²+y²=4的圆心坐标为(4,0),所以圆心(4,0)到直线x-y+4=0的距离d=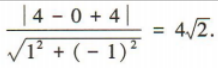
3、若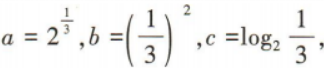 则a,b,c的大小关系为()
则a,b,c的大小关系为()
答 案:D
解 析: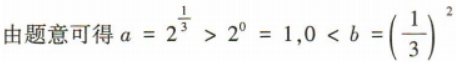
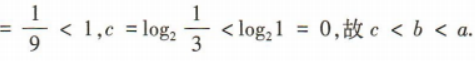
4、已知偶函数f(x)在[0,+∞)上单调递减,且f(1)=0,则满足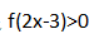 的x的取值范围是()
的x的取值范围是()
- A:(1,2)
- B:(2,+∞)
- C:(-∞,1)∪(2,+∞)
- D:[0,2)
答 案:A
解 析:因为偶函数f(x)在[0,+∞)上单调递减,且f(1)=0,所以函数f(x)在(-∞,0]上单调递增,且f(-1)=0,所以
填空题
1、某学校三年级有8个班,甲、乙两人从外地转到该校三年级,学校让他们各自随机选择班级,他们刚好选在同一个班的概率为()
答 案: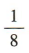
解 析:甲、乙两人各自随机选择班级,所有可能的情况有82=64(种),而他们刚好选在同一个班的情况有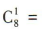 8(种),故他们刚好选在同一个班的概率为
8(种),故他们刚好选在同一个班的概率为
2、设一组样本数据 x1,x2,…,x8的方差为 6,则数据 3x1+1,3x2+1,…,3x8+1的方差是()
答 案:54
解 析:设x1,x2,…,x8的平均数为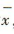 ,则
,则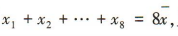 且
且 48,故 3x1+1,3x2+1,…,3x8+1的平均数为
48,故 3x1+1,3x2+1,…,3x8+1的平均数为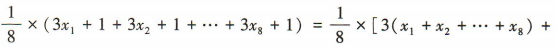
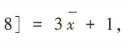 方差为
方差为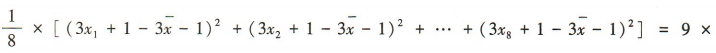
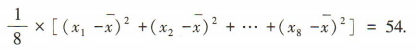
3、已知函数f(x)=x2-2ax+3的值域是[-1,+∞),则a=()
答 案:±2
解 析:易得f(x)=x2-2ax+3=(x-a)2-a2+3,故f(x)min=f(a)=-a2+3=-1,解得a=2或a=-2.
4、某班有 48 名学生,若任选一人是女生的概率是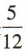 ,则这个班的男生人数是()
,则这个班的男生人数是()
答 案:28
解 析:设这个班的男生人数是x,则这个班的女生人数是48-x. 由题意知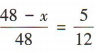 ,解得x=28,所以这个班的男生人数是 28.
,解得x=28,所以这个班的男生人数是 28.
简答题
1、已知关于x的不等式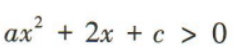 的解集为
的解集为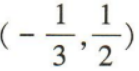 a+c的值.
a+c的值.
答 案:


2、已知双曲线C的中心在原点,焦点在x轴上,焦距为 10,一条渐近线方程为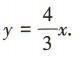 (1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
(1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
答 案:(1)依题意可设C的标准方程为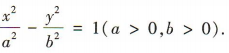 ∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为
∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为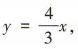 ∴
∴ 又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为
又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为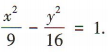 (2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由
(2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由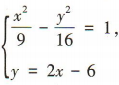 得5x2-54x+117=0,解得
得5x2-54x+117=0,解得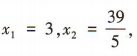 ∴
∴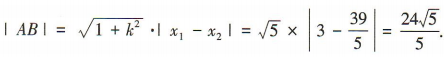
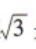 是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.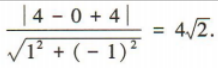
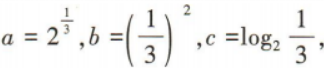 则a,b,c的大小关系为()
则a,b,c的大小关系为()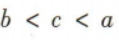
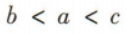
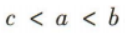
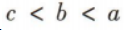
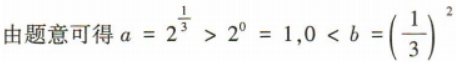
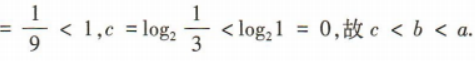
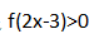 的x的取值范围是()
的x的取值范围是()
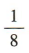
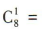 8(种),故他们刚好选在同一个班的概率为
8(种),故他们刚好选在同一个班的概率为
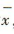 ,则
,则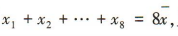 且
且 48,故 3x1+1,3x2+1,…,3x8+1的平均数为
48,故 3x1+1,3x2+1,…,3x8+1的平均数为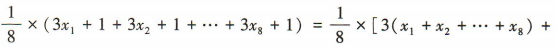
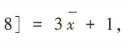 方差为
方差为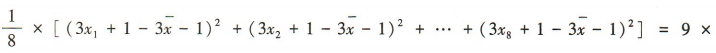
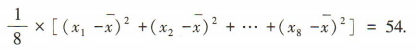
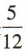 ,则这个班的男生人数是()
,则这个班的男生人数是()
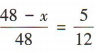 ,解得x=28,所以这个班的男生人数是 28.
,解得x=28,所以这个班的男生人数是 28.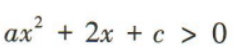 的解集为
的解集为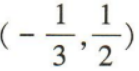 a+c的值.
a+c的值.


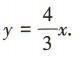 (1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
(1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
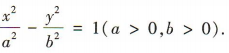 ∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为
∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为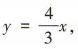 ∴
∴ 又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为
又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为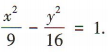 (2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由
(2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由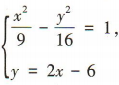 得5x2-54x+117=0,解得
得5x2-54x+117=0,解得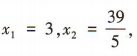 ∴
∴