2024年高职单招《数学(中职)》每日一练试题10月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列运算中,正确的是()
答 案:D
解 析: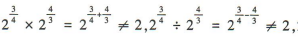
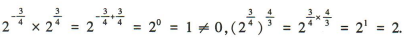 。故A,B,C错误,D正确。
。故A,B,C错误,D正确。
2、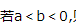 ,则下列不等式不成立的是
,则下列不等式不成立的是
答 案:C
解 析: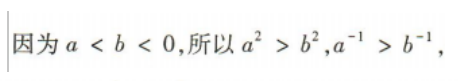
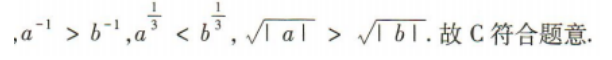
3、已知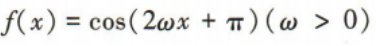 ,则下列说法正确的是()
,则下列说法正确的是()
- A:若f(x)的最小正周期为π,则ω=2
- B:若f(x)的最小正周期为π,则ω=1
- C:若x=0,则f(x)的值为0
- D:若x=0,则f(x)取得最大值-1
答 案:B
解 析: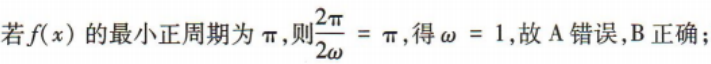 若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.
若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.
4、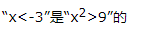
- A:充分非必要条件
- B:必要非充分条件
- C:充分必要条件
- D:非充分非必要条件
答 案:A
解 析:由x2>9得x<-3或x>3,所以“x<-3”是“x2>9”的充分非必要条件
填空题
1、如图,在正方体ABCD-A1B1C1D1中,异面直线D1C与BD 所成角的大小为()
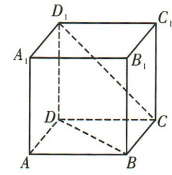
答 案:60°
解 析:在正方体ABCD-A1B1C1D1中,连接B1D1与B1C,如图.易得BD//B1D1,所以 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知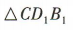 是正三角形,所以
是正三角形,所以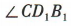 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 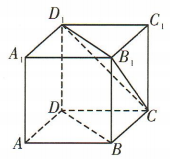
2、若函数y=f(x)在R上是增函数,且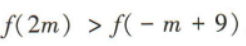 则实数m的取值范围是()
则实数m的取值范围是()
答 案:(3,+∞)
解 析:
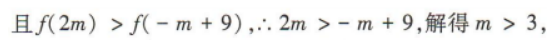 所以实数m的取值范围是(3,+∞)
所以实数m的取值范围是(3,+∞)
3、各棱长都为1的正三棱锥的体积是()
答 案: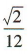
解 析:易知该正三棱锥的底面积为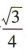 ,高为
,高为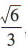 ,故该正三校锥的体积为
,故该正三校锥的体积为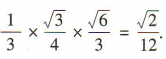
4、不等式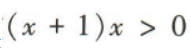 的解集是()
的解集是()
答 案:(-∞,-1)∪(0,+∞)
解 析: 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)
简答题
1、已知Sn是等差数列{an}的前n项和,a6= 0,a3+ a7= 6
(1)求数列{an}的通项公式;
(2)若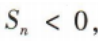 求n的最小值.
求n的最小值.
答 案:(1)设等差数列{an}的公差为d. 因为a6=0,
所以a3+a7=(a6-3d)+(a6+d)=-2d=6,解得d=-3,
所以an=a6+(n-6)d=-3n+18.
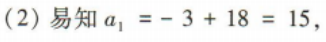
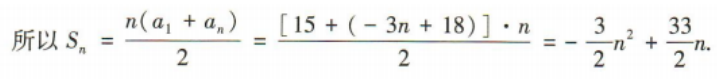
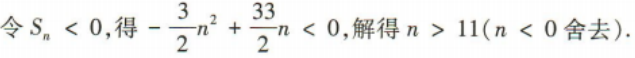

2、已知向量a=(1,x),b=(2x+3,-x).
(1)若a//b,求|a-b|;
(2)若a与b的夹角为锐角,求x的取值范围.
答 案:(1)因为a=(1,x),b=(2x+3,-x),a//b, 所以-x=x(2x+3),解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),
所以a-b=(-2,0),
所以|a-b|=2;
当x=-2时,a=(1,-2),b=(-1,2),
所以a-b=(2,-4),
所以|a-b|=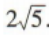 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=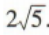 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
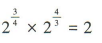
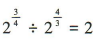
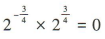
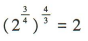
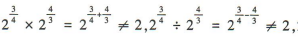
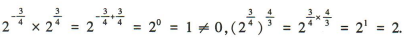 。故A,B,C错误,D正确。
。故A,B,C错误,D正确。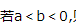 ,则下列不等式不成立的是
,则下列不等式不成立的是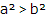
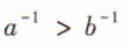
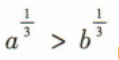
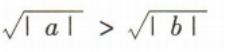
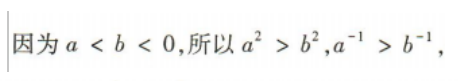
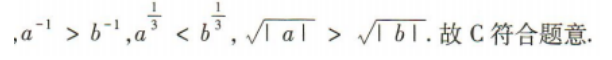
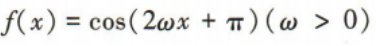 ,则下列说法正确的是()
,则下列说法正确的是()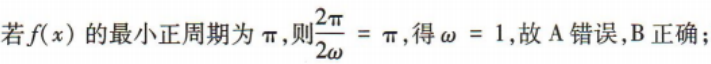 若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.
若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.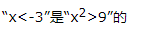

 为异面直线D1C与BD所成的角.易知
为异面直线D1C与BD所成的角.易知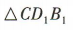 是正三角形,所以
是正三角形,所以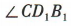 =60°,所以异面直线 D1C与 BD 所成角的大小为 60°.
=60°,所以异面直线 D1C与 BD 所成角的大小为 60°. 
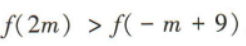 则实数m的取值范围是()
则实数m的取值范围是()
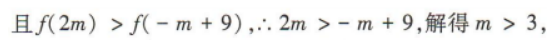 所以实数m的取值范围是(3,+∞)
所以实数m的取值范围是(3,+∞)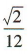
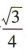 ,高为
,高为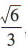 ,故该正三校锥的体积为
,故该正三校锥的体积为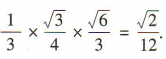
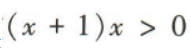 的解集是()
的解集是() 所以原不等式的解集为(-∞,-1)∪(0,+∞)
所以原不等式的解集为(-∞,-1)∪(0,+∞)
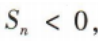 求n的最小值.
求n的最小值.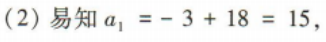
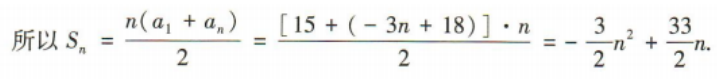
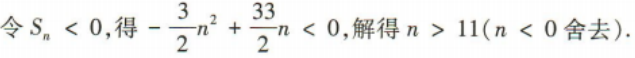

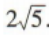 .
综上,|a-b|=2或Ia-bl=
.
综上,|a-b|=2或Ia-bl=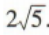 .
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).
.
(2)由a与b的夹角为锐角,得a·b=2x+3-x2>0且-x≠x(2x+3),解得-1<x<3且x≠0,所以x的取值范围是(-1,0)∪(0,3).


