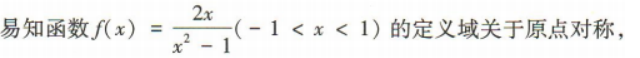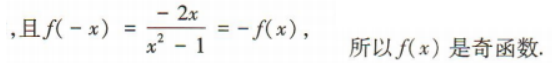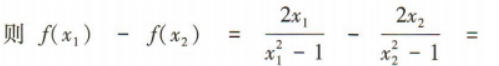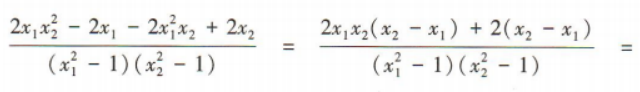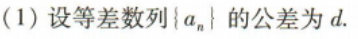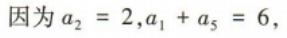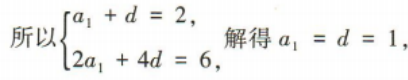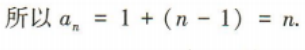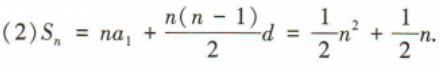2024年高职单招《数学(中职)》每日一练试题10月01日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知函数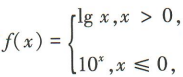 若
若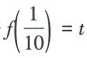 ,则f(t)=()
,则f(t)=()
- A:-1
- B:
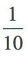
- C:1
- D:10
答 案:B
解 析:因为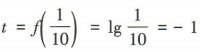 ,所以
,所以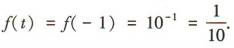
2、已知抛物线的方程为y2 =- 6x,过点(0,3)且倾斜角为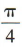 的直线l交抛物线于A,B两点,则线段 AB的中点坐标为()
的直线l交抛物线于A,B两点,则线段 AB的中点坐标为()
- A:(-6,-3)
- B:(-3,-6)
- C:(6.3)
- D:(3,6)
答 案:A
解 析:因为直线l的倾斜角为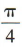 ,所以直线l的斜率
,所以直线l的斜率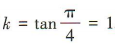 .又直线l过点(0,3),所以直线l的方程为y=x+3.设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0).由
.又直线l过点(0,3),所以直线l的方程为y=x+3.设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0).由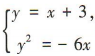 得x2+12x+9=0,所以x1+x2=-12,所以
得x2+12x+9=0,所以x1+x2=-12,所以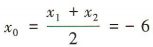 ,将x0=-6代入y=x+3得y0=-3,所以线段AB 的中点坐标为(-6,- 3).
,将x0=-6代入y=x+3得y0=-3,所以线段AB 的中点坐标为(-6,- 3).
3、A,B,C,D四人站成一排,如果A与B相邻,那么不同的排法共有
答 案:B
解 析:先安排 A,B,共有 种方法;再把他们看作一整体,与其他人一起安排,共有
种方法;再把他们看作一整体,与其他人一起安排,共有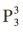 种方法,故不同的排法种数为
种方法,故不同的排法种数为 
4、已知向量a=(5,1),b=(x,-2),若a⊥b,则x=()
- A:-2
- B:-1
- C:
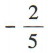
- D:
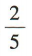
答 案:D
解 析:因为a=(5,1),b=(x,-2),a⊥b,所以a·b=5x-2=0,解得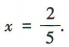
填空题
1、已知0是正方形ABCD的中心,则向量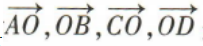 是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
答 案:④
解 析:根据向量的有关概念及正方形的性质,可得向量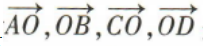 是模都相等的向量
是模都相等的向量
2、一个数分别加上20,50,100后得到的三个数成等比数列,则这个数为()
答 案:25
解 析:设所求的数为x.根据题意得(x+50)2=(x+20)(x+100),解得x=25.
3、已知函数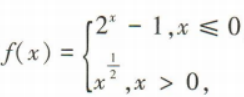 若f(m)=3,则m=()
若f(m)=3,则m=()
答 案:9
解 析: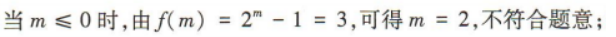
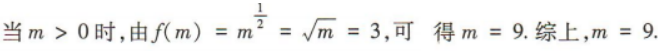
4、若函数y=2sinx+a的最大值为-2,则a的值为()
答 案:-4
解 析:由-1≤sinx≤1,可知当sinx=1时,y=2sinx+a取得最大值2+a.由题意知2+a=-2,解得a=-4.
简答题
1、已知函数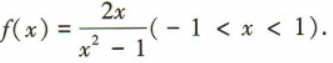 (1)判断函数f(x)的奇偶性,并说明理由;
(2)判断函数f(x)的单调性并证明.
(1)判断函数f(x)的奇偶性,并说明理由;
(2)判断函数f(x)的单调性并证明.
答 案:(1)f(x)是奇函数,理由如下: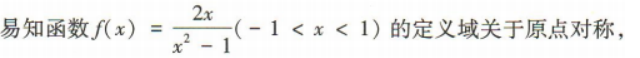
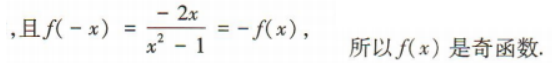

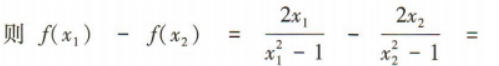
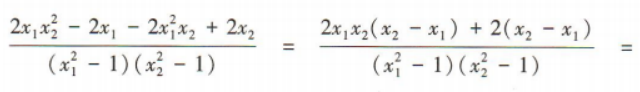

2、已知等差数列{an}中,a2=2,a1+a5=6.
(1)求{an}的通项公式;
(2)求数列{an}的前n项和Sn.
答 案: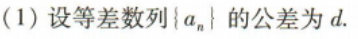
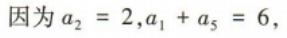
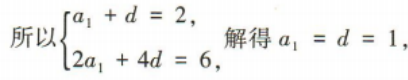
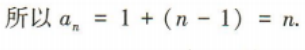
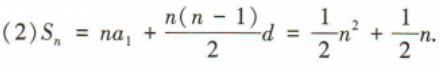
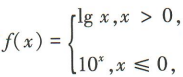 若
若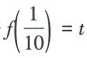 ,则f(t)=()
,则f(t)=()
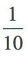
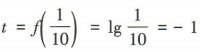 ,所以
,所以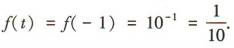
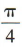 的直线l交抛物线于A,B两点,则线段 AB的中点坐标为()
的直线l交抛物线于A,B两点,则线段 AB的中点坐标为()
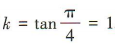 .又直线l过点(0,3),所以直线l的方程为y=x+3.设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0).由
.又直线l过点(0,3),所以直线l的方程为y=x+3.设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0).由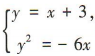 得x2+12x+9=0,所以x1+x2=-12,所以
得x2+12x+9=0,所以x1+x2=-12,所以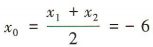 ,将x0=-6代入y=x+3得y0=-3,所以线段AB 的中点坐标为(-6,- 3).
,将x0=-6代入y=x+3得y0=-3,所以线段AB 的中点坐标为(-6,- 3). 种方法;再把他们看作一整体,与其他人一起安排,共有
种方法;再把他们看作一整体,与其他人一起安排,共有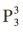 种方法,故不同的排法种数为
种方法,故不同的排法种数为 
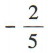
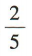
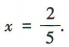
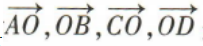 是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量
是().(填序号)
①平行向量;②相等向量;③有相同终点的向量;④模都相等的向量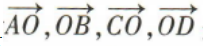 是模都相等的向量
是模都相等的向量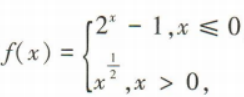 若f(m)=3,则m=()
若f(m)=3,则m=()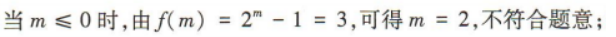
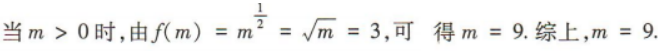
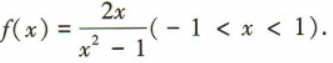 (1)判断函数f(x)的奇偶性,并说明理由;
(2)判断函数f(x)的单调性并证明.
(1)判断函数f(x)的奇偶性,并说明理由;
(2)判断函数f(x)的单调性并证明.