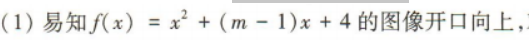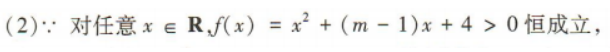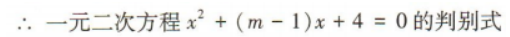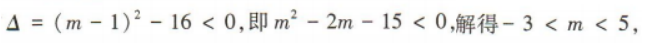2024年高职单招《数学(中职)》每日一练试题09月25日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、“x²-x-6=0”是“x=3”的()
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:B
解 析:由x²-x-6=0,得x=-2或x=3.若x²-x-6=0,则不一定有x=3,故充分性不满足.若x=3,则x²-x-6=0,故必要性成立.综上所述,“x²-x-6=0”是“x=3”的必要不充分条件.
2、在等差数列{an}中,a3+a5=8,则a1+a2+…+a7=()
答 案:C
解 析:∵{an}是等差数列,∴a3+a5=2a4=8,:a4=4,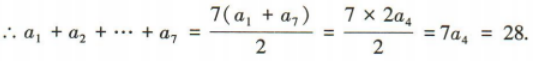
3、下列运算中,正确的是()
答 案:D
解 析: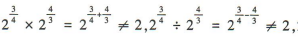
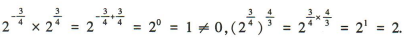 。故A,B,C错误,D正确。
。故A,B,C错误,D正确。
4、在等比数列{an}中,若a3a5=16,则a4=()
答 案:D
解 析: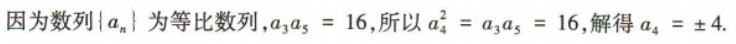
填空题
1、已知 a1 ,a2的平均数为 6.5,且 a3,a4,a5的平均数为9,则 a1 ,a2,a3,a4,a5的平均数为()
答 案:8
解 析:因为a1 ,a2的平均数为6.5,所以 a1+a2= 13. 因为a3,a4,a5的平均数为9,所以a3+a4+a5= 27,所以a1,a2,a3,a4,a5的平均数为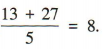
2、已知函数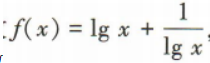 则f(100)=()
则f(100)=()
答 案: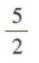
解 析: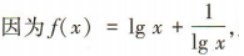
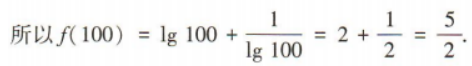
3、函数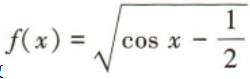 的定义域为()
的定义域为()
答 案: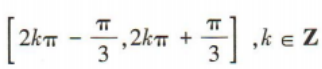
解 析:
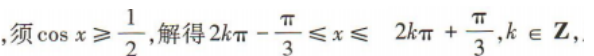
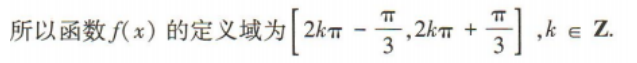
4、已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)=()
答 案:
解 析: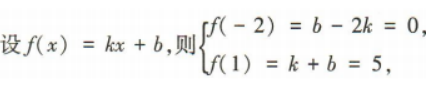

简答题
1、如图,已知四棱锥P-ABCD的底面ABCD是矩形, ,AB=PD=4,AD=2,点E,F分别是 AB,PC的中点.
,AB=PD=4,AD=2,点E,F分别是 AB,PC的中点.
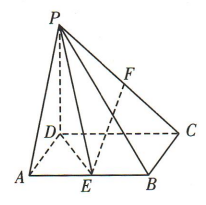 (1)证明:EF//平面PAD.
(1)证明:EF//平面PAD.
(2)求三棱锥E-PAD 的体积.
答 案: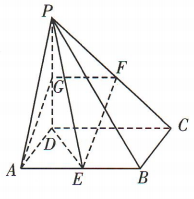 (1)取 PD 中点 G,连接 GF,AG.
因为G,F分别是PD,PC的中点,
所以
(1)取 PD 中点 G,连接 GF,AG.
因为G,F分别是PD,PC的中点,
所以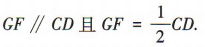 又因为底面 ABCD 为矩形,E为AB 中点,
所以
又因为底面 ABCD 为矩形,E为AB 中点,
所以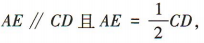 所以GF//AE 且GF = AE,
所以四边形 CFEA 为平行四边形,
所以 GA // EF.
又
所以GF//AE 且GF = AE,
所以四边形 CFEA 为平行四边形,
所以 GA // EF.
又 所以EF//平面PAD.
(2)因为
所以EF//平面PAD.
(2)因为 所以 PD 为三棱锥P-AED 的高.
又
所以 PD 为三棱锥P-AED 的高.
又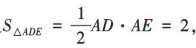 所以
所以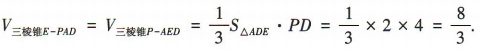
2、已知函数f(x)=x2+(m-1)x+4,其中m为常数.
(1)若函数f(x)在区间(-∞,0)上单调递减,求实数m的取值范围;
(2)若对任意x∈R,都有 求实数m的取值范围.
求实数m的取值范围.
答 案: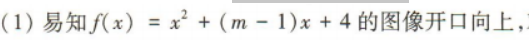

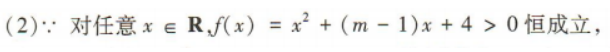
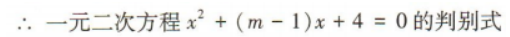
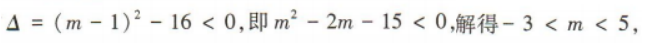

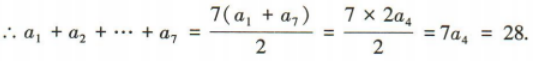
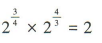
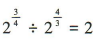
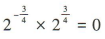
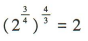
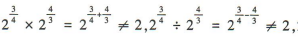
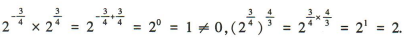 。故A,B,C错误,D正确。
。故A,B,C错误,D正确。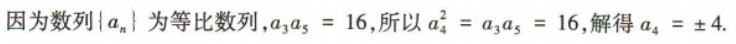
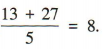
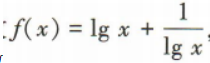 则f(100)=()
则f(100)=()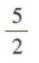
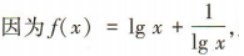
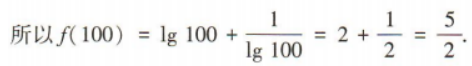
 的定义域为()
的定义域为()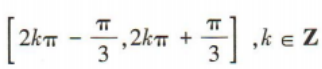

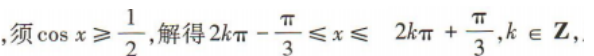
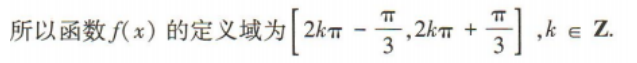

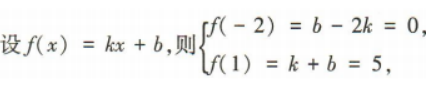

 ,AB=PD=4,AD=2,点E,F分别是 AB,PC的中点.
,AB=PD=4,AD=2,点E,F分别是 AB,PC的中点.
 (1)证明:EF//平面PAD.
(1)证明:EF//平面PAD. (1)取 PD 中点 G,连接 GF,AG.
因为G,F分别是PD,PC的中点,
所以
(1)取 PD 中点 G,连接 GF,AG.
因为G,F分别是PD,PC的中点,
所以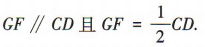 又因为底面 ABCD 为矩形,E为AB 中点,
所以
又因为底面 ABCD 为矩形,E为AB 中点,
所以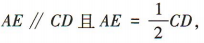 所以GF//AE 且GF = AE,
所以四边形 CFEA 为平行四边形,
所以 GA // EF.
又
所以GF//AE 且GF = AE,
所以四边形 CFEA 为平行四边形,
所以 GA // EF.
又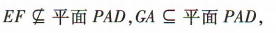 所以EF//平面PAD.
(2)因为
所以EF//平面PAD.
(2)因为 所以 PD 为三棱锥P-AED 的高.
又
所以 PD 为三棱锥P-AED 的高.
又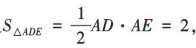 所以
所以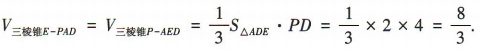
 求实数m的取值范围.
求实数m的取值范围.