2024年高职单招《数学(中职)》每日一练试题09月23日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知a,b是单位向量,则下列结论中正确的是()
- A:a=b
- B:a=-b
- C:a//b
- D:|a|2=|b|2
答 案:D
解 析:因为a,b都是单位向量,所以a,b模相等,但方向不确定,所以a,b不一定是共线向量,故A,B,C错误;因为|a|=|b|=1,所以|a|2=|b|2=1,故D正确.
2、不等式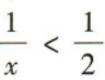 的解集是()
的解集是()
- A:(-∞,2)
- B:(2,+∞)
- C:(0,2)
- D:(-∞,0)∪(2,+∞)
答 案:D
解 析: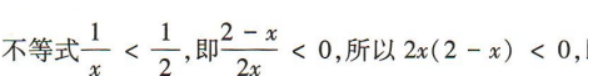
 故原不等式的解集为(-∞,0)∪(2,+∞)
故原不等式的解集为(-∞,0)∪(2,+∞)
3、“a>1”是“a>-1”的
- A:充分非必要条件
- B:必要非充分条件
- C:充分必要条件
- D:非充分非必要条件
答 案:A
解 析:由a>1能推出a>-1,由a>-1不能推出a>1,所以“a>1”是“a>-1”的充分非必要条件
4、函数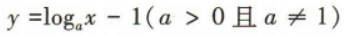 的图像过定点()
的图像过定点()
- A:(0,-1)
- B:(1,-1)
- C:(1,1)
- D:(1,0)
答 案:B
解 析:令x=1,则y=loga1-1=-1,所以函数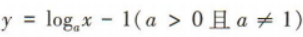 的图像过定点(1,-1).
的图像过定点(1,-1).
填空题
1、已知函数f(x)=x2-2ax+3的值域是[-1,+∞),则a=()
答 案:±2
解 析:易得f(x)=x2-2ax+3=(x-a)2-a2+3,故f(x)min=f(a)=-a2+3=-1,解得a=2或a=-2.
2、若函数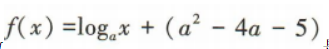 是对数函数,则a=()
是对数函数,则a=()
答 案:5
解 析: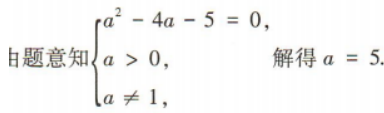
3、已知向量a=(6,2),b=(3,6),则a与b的夹角为()
答 案: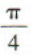
解 析: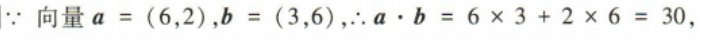
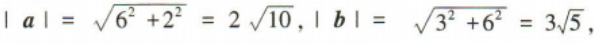
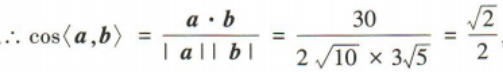
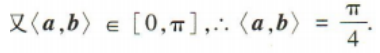
4、如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则以下四个结论正确的是().(填写正确结论的编号)① 直线 AM 与CC1是相交直线;②直线 AM 与 BN 是平行直线;③ 直线 BN 与MB1是异面直线;④ 直线 AM 与DD1是异面直线.
答 案:③④
解 析:易知A,M,C1均在平面AD1C1B中,但 所以直线AM与 CC1是异面直线.同理,AM 与 BN是异面直线,BN与 MB1是异面直线,AM 与 DD1是异面直线,故 ①② 错误,③④ 正确.
所以直线AM与 CC1是异面直线.同理,AM 与 BN是异面直线,BN与 MB1是异面直线,AM 与 DD1是异面直线,故 ①② 错误,③④ 正确.
简答题
1、已知p:x2-8x-20≤0,q:1-m≤x≤1+m(m>0).若p是q的必要不充分条件,求实数m的范围.
答 案:由x2-8x-20≤0得-2≤x≤10,即p:-2≤x≤10. ∵p是q的必要不充分条件,q:1-m≤x≤1+m(m>0),
2、已知圆C:(x-2)2+(y-3)2= 4.
(1)圆外有一点P(4,-1),过点P作直线l与圆C相切,求直线l的方程;
(2)若直线x+y+m=0被圆C所截得的弦长为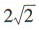 ,求m的值.
,求m的值.
答 案:(1)易知圆C:(x-2)2+(y-3)2= 4的圆心为(2,3),半径r= 2. 当直线l的斜率不存在时,直线l的方程为x=4,圆心到直线x=4的距离为2=r,符合题意.
当斜率存在时,设直线l的方程为kx-y-4k-1=0.
因为直线l与圆C相切,
所以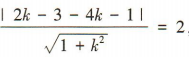 ,解得
,解得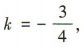 所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离
所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离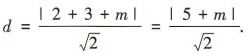 因为直线x+y+m=0被圆C所截得的弦长为
因为直线x+y+m=0被圆C所截得的弦长为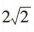 ,
所以
,
所以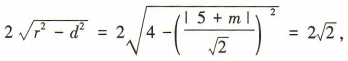 所以m=-3或m=-7.
所以m=-3或m=-7.
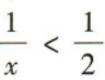 的解集是()
的解集是()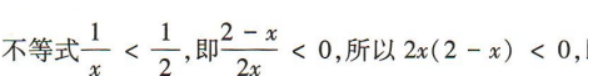
 故原不等式的解集为(-∞,0)∪(2,+∞)
故原不等式的解集为(-∞,0)∪(2,+∞)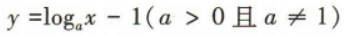 的图像过定点()
的图像过定点()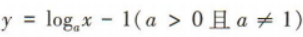 的图像过定点(1,-1).
的图像过定点(1,-1).
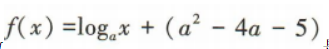 是对数函数,则a=()
是对数函数,则a=()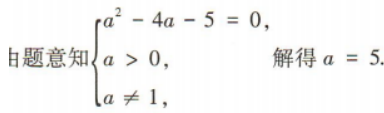
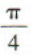
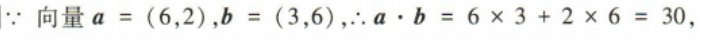
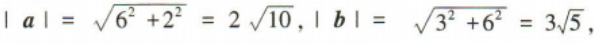
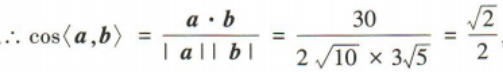
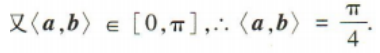

 所以直线AM与 CC1是异面直线.同理,AM 与 BN是异面直线,BN与 MB1是异面直线,AM 与 DD1是异面直线,故 ①② 错误,③④ 正确.
所以直线AM与 CC1是异面直线.同理,AM 与 BN是异面直线,BN与 MB1是异面直线,AM 与 DD1是异面直线,故 ①② 错误,③④ 正确.
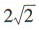 ,求m的值.
,求m的值.
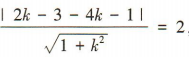 ,解得
,解得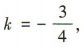 所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离
所以l的方程为3x+4y-8=0.
综上,直线l的方程为x=4或3x+4y-8=0.
(2)易得圆心(2,3)到直线x+y+m=0的距离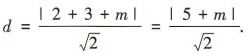 因为直线x+y+m=0被圆C所截得的弦长为
因为直线x+y+m=0被圆C所截得的弦长为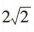 ,
所以
,
所以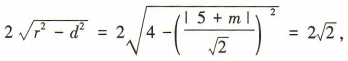 所以m=-3或m=-7.
所以m=-3或m=-7.


