2024年高职单招《数学(中职)》每日一练试题09月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知tanα=2,则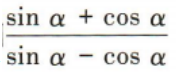 ()
()
答 案:B
解 析:
2、sin10°cos50°+cos10°sin50°=()
答 案:C
解 析:sin10°cos50°+cos10°sin50°=sin(10°+50°)=sin60°=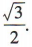
3、下列与集合{2 023,1}表示同一集合的是()
- A:( 2 023,1)
- B:{(x,y)|x=2 023,y=1}
- C:{x|x2-2 024x+2 023=0}
- D:{(2 023,1)}
答 案:C
解 析:方程x2-2 024x+2 023=0的解为x=2 023或x=1,所以|x|x2-2 024x+2 023=0}={2 023,1}, 故{x|x2-2 024x+2 023=0}与集合{2 023,1}表示同一集合.
4、若双曲线的方程为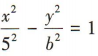 ,渐近线方程为
,渐近线方程为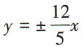 ,则焦距为()
,则焦距为()
答 案:B
解 析:由双曲线的方程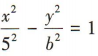 ,得双曲线的渐近线方程为
,得双曲线的渐近线方程为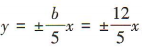 ,所以b=12,又a=5.所以c=
,所以b=12,又a=5.所以c=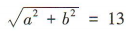 ,所以焦距 2c = 26.
,所以焦距 2c = 26.
填空题
1、若关于x的不等式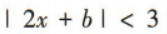 的解集为
的解集为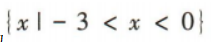 则b的值为
则b的值为
答 案:3
解 析:
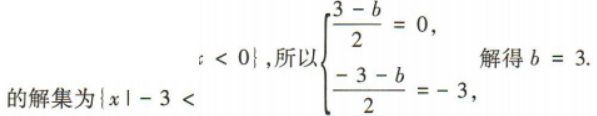
2、已知向量a=(1,2),b=(-3,1),则(a·b)(a-b)=()
答 案:(-4,-1)
解 析:由a=(1,2),b=(-3,1),得a·b=-3×1+1×2=-1,a-b=(4,1),所以(a·b)(a-b)=(-4,-1).
3、(1+x)5的展开式中,二项式系数的和是()
答 案:32
解 析:令x=1,得二项式系数的和为25= 32.
4、盒子中有散落的黑白棋子若干粒,已知从中取出2粒都是黑子的概率是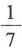 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是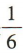 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
答 案: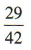
解 析:由题意,任意取出2粒棋子,不考虑先后顺序,一共有2粒都是黑子,2粒都是白子和一粒黑子一粒白子3 种可能.设事件A =“取出2粒都是黑子”,事件B=“取出2粒都是白子”,事件C=“取出2粒恰好是一粒黑子一粒白子”,则A,B,C两两互斥.由已知得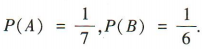 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=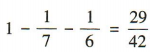 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是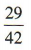
简答题
1、已知a,b,c分别为△ABC的内角A,B,C的对边,且c2=2ab.
(1)若C=90°,且a=1,求△ABC的面积;
(2)若sinA=sinC,求cosC的值.
答 案: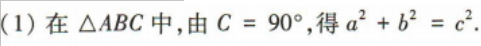
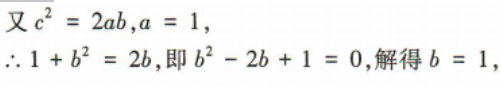
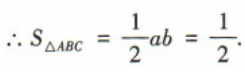

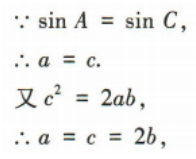
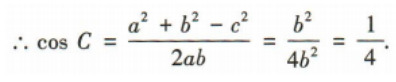
2、某物业管理公司有75套公寓对外出租,经市场调查发现,每套公寓租价为2500元时,可以全部租出,租价每上涨100元就会少租出一套公寓,问:每套公寓租价为多少元时,租金总收入最大?最大收入为多少元?
答 案:设每套公寓租价上涨100x元,则每套公寓的租价为(2500+100x)元,共租出(75-x)套. 依题意,租金总收入y=(2500+100x)(75-x)=-100x2+5000x+187500=-100(x-25)2+250000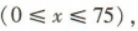 则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
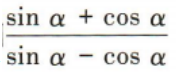 ()
()
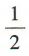
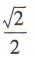
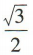
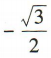
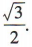
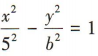 ,渐近线方程为
,渐近线方程为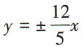 ,则焦距为()
,则焦距为()
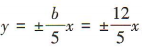 ,所以b=12,又a=5.所以c=
,所以b=12,又a=5.所以c=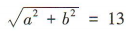 ,所以焦距 2c = 26.
,所以焦距 2c = 26.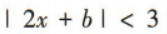 的解集为
的解集为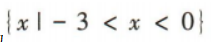 则b的值为
则b的值为
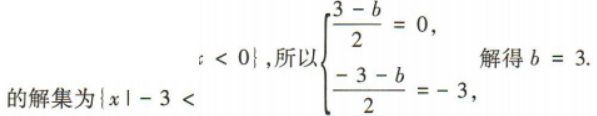
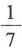 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是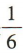 ,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
,则从中任意取出2粒恰好是一粒黑子一粒白子的概率是()
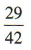
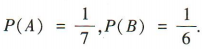 ∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=
∵P(AUBUC)= P(A)+ P(B)+ P(C) = 1,∴P(C)=1-P(A)-P(B)=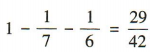 ,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是
,∴从中任意取出2粒恰好是一粒黑子一粒白子的概率是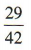
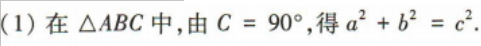
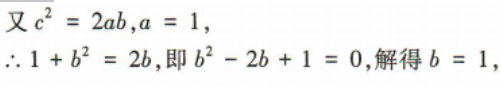
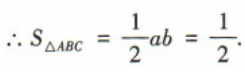

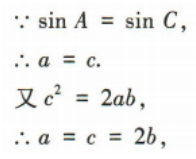
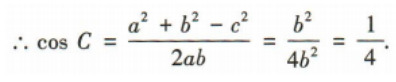
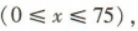 则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.
则当x=25时,y取得最大值250000.
故当每套公寓租价为5000元时,租金总收入最大,最大收入为250000元.


