2024年高职单招《数学(中职)》每日一练试题09月16日

2024年高职单招《数学(中职)》每日一练试题09月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列函数中，是偶函数的为（）  

• A：f(x)=x
• B：
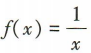
• C：f(x)=x²
• D：f(x)=sinx

答 案：C

解 析：函数f(x)=x的定义域为R,f(-x)=-x=-f(x),所以f(x)是奇函数，故A不符合题意；函数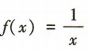的定义域为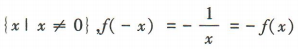,所以f(x)是奇函数，故B不符合题意；函数f(x)=x²的定义域为R,f(-x)=(-x)²=f(x),所以f(x)是偶函数，故C符合题意；函数f(x)=sinx的定义域为R,f(-x)=sin(-x)=-sinx=-f(x),所以f(x)是奇函数，故D不符合题意.

2、sin70°sin10°+cos10°cos70°=（）

• A：
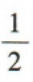
• B：
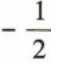
• C：
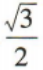
• D：

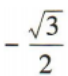
答 案：A

解 析：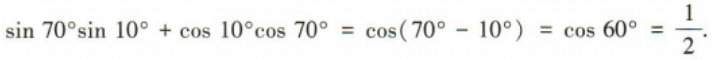

3、若函数f(x)在R上是减函数，且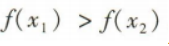,则下列结论正确的是（）

• A：
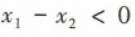
• B：
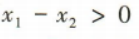
• C：
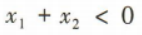
• D：

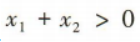
答 案：A

解 析：由f(x)在R上是减函数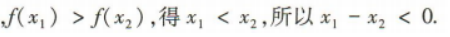

4、不等式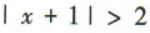的解集为（）

• A：
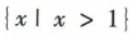
• B：
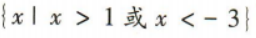
• C：
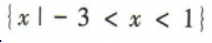
• D：

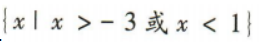
答 案：B

解 析：

填空题

1、(2+3i)-(4 +5i)=（）.(其中i是虚数单位)  

答 案：-2-2i

解 析：易得(2+3i)-(4+5i)=-2-2i.

2、已知函数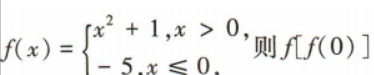的值为（）

答 案：-5

解 析：由题意得f(0)=-5,所以f[f(0)]=f(-5)=-5.

3、在复平面内,如果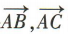对应的复数分别是5+4i,-2+3i,那么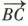对应的复数为（）  

答 案：-7-ì

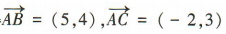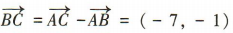解 析：由题意得,所以,所以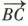对应的复数为-7 -i.

4、某医疗机构有4名新冠疫情防控志愿者,现要从这4人中选3个人去3个不同的社区进行志愿服务则不同的安排方法共有（）种.  

答 案：24

解 析：由题意可分两步,第一步,从4名新冠疫情防控志愿者中选出3人,共有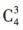种方法:第二步,选出的3人去3 个不同的社区,共有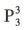种方法,根据分步乘法计数原理可知不同的安排方法共有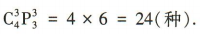

简答题

1、若关于x的不等式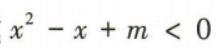的解集是∅,求实数m的取值范围.

答 案：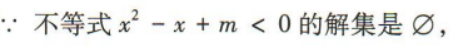

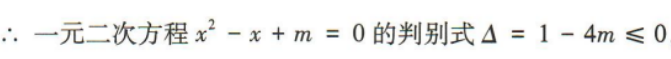
2、若集合A={x | x²-6x+5=0},写出集合A的所有子集.  

答 案：易得A={1,5} 故A的所有子集为∅,{1},[5},{1,5}