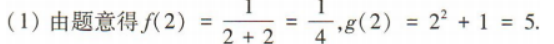2024年高职单招《数学(中职)》每日一练试题09月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、复数 i2022=()
答 案:D
解 析:易得i2022=(i4)505•i2=1x(-1)=-1.
2、不等式组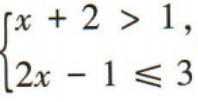 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()
答 案:B
解 析:由x+2>1,得x>-1,由2x-1≤3,得x≤2,∴不等式组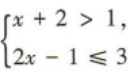 的解集为-1<x≤2,:.在数轴上表示正确的是B.
的解集为-1<x≤2,:.在数轴上表示正确的是B.
3、在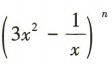 的展开式中,所有二项式系数和为 64,则n的值为()
的展开式中,所有二项式系数和为 64,则n的值为()
答 案:A
解 析:因为在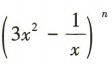 的展开式中,所有二项式系数和为64,所以2n=64,解得n=6.
的展开式中,所有二项式系数和为64,所以2n=64,解得n=6.
4、不等式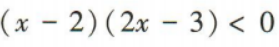 的解集是()
的解集是()
- A:
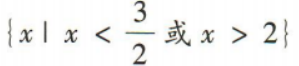
- B:R
- C:
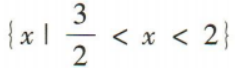
- D:∅
答 案:C
解 析:

填空题
1、袋中装有大小、形状完全相同的6个白球,4个红球,从中任取一球,则取到白球的概率为()
答 案: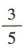
解 析:因为一共有 10 个球,所以从中任取一球的基本事件有 10个,又有6个白球,所以取到白球的基本事件有6个,所以取到白球的概率为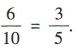
2、已知函数f(x)是R上的奇函数,且在(0,+∞)上单调递减,f(-5)=0,则不等式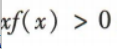 的解集是()
的解集是()
答 案:(-5,0)∪(0,5)
解 析:根据题意画出f(x)的大致图像如图所示.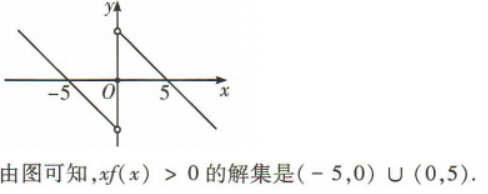
3、已知奇函数f(x)在[-3,0]上单调递减,且f(-3)=2,则f(x)在[0,3]上的最小值为()
答 案:-2
解 析:因为f(x)为奇函数,且在[-3,0]上单调递减,所以f(x)在[0,3]上单调递减,所以f(x)在[0,3]上的最小值为f(3).由f(x)是奇函数,f(-3)=2得f(3)=-f(-3)=-2,所以f(x)在[0,3]上的最小值为-2
4、已知数据x,8,y的平均数为8,则数据9,5,x,y,15 的平均数为()
答 案:9
解 析:因为x,8,y的平均数为8,所以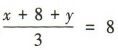 ,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为
,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为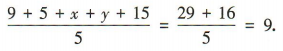
简答题
1、已知f(x)=2x2+n,且f(1)=4.
(1)求f(x)的解析式;
(2)判断f(x)的奇偶性并写出其单调区间;
(3)若关于x的方程f(x)=kx有两个不相等的实数根,求实数k的取值范围.
答 案:(1)由f(1)=4得f(1)=2+n=4, 所以n=2,
所以f(x)=2x2+2.
(2)易知函数f(x)的定义域为R,关于原点对称,且f(-x)=2(-x)2+2=2x2+2=f(x),
所以函数f(x)为偶函数.
易知f(x)=2x2+2图像的对称轴为直线x=0,且开口向上,
所以函数f(x)的单调递减区间为(-∞,0],单调递增区间为[0,+∞).
(3)因为方程f(x)=kx有两个不相等的实数根,
所以2x2-kx+2=0有两个不相等的实数根,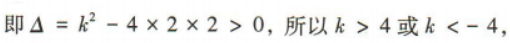 故实数k的取值范围为(-∞,-4)∪(4,+∞).
故实数k的取值范围为(-∞,-4)∪(4,+∞).
2、已知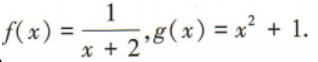 (1)求f(2),g(2)的值;
(2)求f[g(3)]的值;
(3)求f(x),g(x)的值域.
(1)求f(2),g(2)的值;
(2)求f[g(3)]的值;
(3)求f(x),g(x)的值域.
答 案: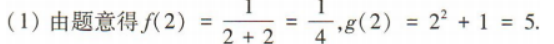



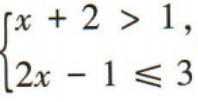 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()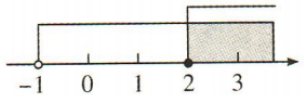

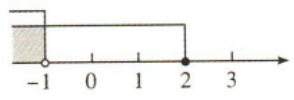
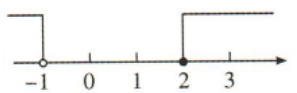
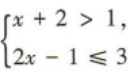 的解集为-1<x≤2,:.在数轴上表示正确的是B.
的解集为-1<x≤2,:.在数轴上表示正确的是B.
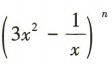 的展开式中,所有二项式系数和为 64,则n的值为()
的展开式中,所有二项式系数和为 64,则n的值为()
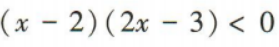 的解集是()
的解集是()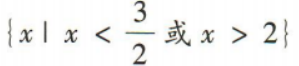
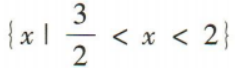


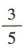
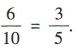
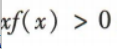 的解集是()
的解集是()
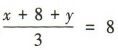 ,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为
,解得x+y= 16. 所以数据 9,5,x,y,15 的平均数为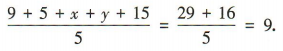
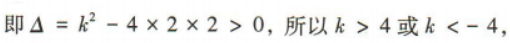 故实数k的取值范围为(-∞,-4)∪(4,+∞).
故实数k的取值范围为(-∞,-4)∪(4,+∞).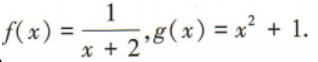 (1)求f(2),g(2)的值;
(2)求f[g(3)]的值;
(3)求f(x),g(x)的值域.
(1)求f(2),g(2)的值;
(2)求f[g(3)]的值;
(3)求f(x),g(x)的值域.