课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年高职单招《数学》每日一练试题09月09日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、零和负数没有对数。()
答 案:对
解 析:零没有对数。在实数范围内,负数无对数。
2、方程x2+y2=9表示圆心在原点,半径为3的一个圆。()
答 案:对
单选题
1、已知奇函数y=f(x)在其定义域上是增函数,那么y=f(-x)在它的定义域上()
- A:既是奇函数,又是增函数
- B:既是奇函数,又是减函数
- C:既是偶函数,又是先减后增的函数
- D:既是偶函数,又是先增后减的函数
答 案:B
2、圆心为(1,2),且过(0,0)的圆的方程为()
- A:

- B:x2+y2=4
- C:(x-1)2+(y-2)2=5
- D:

答 案:C
多选题
1、下列四个命题中正确的是()
- A:与圆有公共点的直线是该圆的切线
- B:垂直于圆的半径的直线是该圆的切线
- C:到圆心的距离等于半径的直线是该圆的切线
- D:过圆直径的端点,垂直于此直径的直线是该圆的切线
答 案:CD
解 析:A中,与圆有两个公共点的直线,是圆的割线,故该选项不符合题意;B中,应经过此半径的外端,故该选项不符合题意;C中,根据切线的判定方法,故该选项符合题意;D中,根据切线的判定方法,故该选项符合题意。故选:CD。
2、已知函数y=1/2sin2x则()
- A:函数最大值为2
- B:函数最大值为1/2
- C:周期
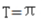
- D:周期
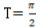
答 案:BC
解 析:A:sin2x最大值为1,则y=1/2sin2x的最大值为1/2,故A错B对。C:T=2π/W=2π/2=π,故C对D错
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1.
(2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1.
(3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
填空题
1、学校文艺队每个队员唱歌、跳舞至少会一门,已知会唱歌的有5人,会跳舞的有7人,现从中选3人,且至少要有一位既会唱歌又会跳舞的概率是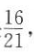 ,则该队有()人.
,则该队有()人.
答 案:9
解 析:设该队既会唱歌又会跳舞的有x人,则该队共有(12-x)人,且只会唱歌或只会跳舞的有(12-2x)人.记“从中选3人,至少要有一位既会唱歌又会跳舞”为事件A,则事件A的对立事件A是“从中选的3人都只会唱歌或只会跳舞”.因为 ,所以
,所以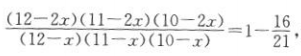 ,解得x=3,所以12一x=9,即该队共有9人.
,解得x=3,所以12一x=9,即该队共有9人.
2、一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为______
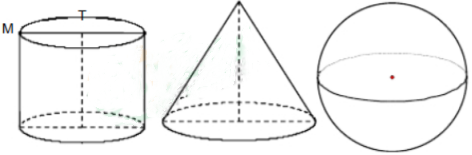
答 案:3:1:2
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!


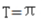
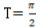

 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合. 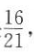 ,则该队有()人.
,则该队有()人. ,所以
,所以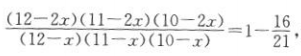 ,解得x=3,所以12一x=9,即该队共有9人.
,解得x=3,所以12一x=9,即该队共有9人.



