2024年高职单招《数学》每日一练试题09月02日

2024年高职单招《数学》每日一练试题09月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、满足不等式a≤x≤b的实数x的集合叫闭区间，表示为（a，b）。（）  

答 案：错

2、已知1/a>1/b,则a＜b。（）  

答 案：错

解 析：如果a为正b为负则后面不成立

单选题

1、  

• A：等边三角形
• B：等腰三角形
• C：直角三角形
• D：等腰直角三角形

答 案：A

2、已知函数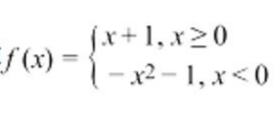，若f（x）=-10，则x=________  

• A：-3
• B：-4
• C：-2
• D：-1

答 案：A

解 析：先看分段函数，x≥0的时候，x+1≥1，所以不可能为负数，所以一定是第二段x＜0.所以代入得f（x）=-10=-x^2-1。得x的值。

多选题

1、已知点P到圆O上的点的最大距离是7cm，最小距离是1m，则圆O的半径是（）  

• A：4cm
• B：3cm
• C：5cm
• D：6cm

答 案：AB

2、已知等差数列{a_n}的前n项和为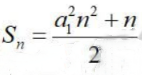，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

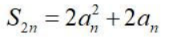
答 案：ABC

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、双曲线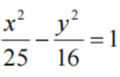的渐近线方程为_______  

答 案：y=±4/5x

解 析：双曲线的渐近线方程y=±b/ax。由题意可知a=5，b=4

2、函数y= log₂ (x²-4x+3) 的单调递减区间是______.

答 案：(-∞，1)

解 析：由x²-4x+3>0,得x< 1或x>3.
令g(x)=x²-4x+3 ,其对称轴方程为x= 2.
所以函数g(x)=x²-4x+3在(3, +∞)上为单调递增,在（-∞，1）上单调递减
又函数y= log₂ t 为增函数，同增异减
所以函数y = log₂(x² - 4x + 3)的递减区间为(-∞，1).
故答案为(-∞，1).