2024年高职单招《数学》每日一练试题07月19日
2024-07-19 14:33:34 来源:吉格考试网
2024年高职单招《数学》每日一练试题07月19日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、过点(0,1)且与直线2x-y=0垂直的直线方程的一般式是y=-2x+1。()
答 案:错
2、若直线y=2x-1与直线y=kx+1平行,则k=2.()
答 案:对
解 析:直线y=2x-1与直线y=kx+1平行,所以k=2。
单选题
1、已知a,b,c,d是公比为2的等比数列,则c/a=()
- A:2
- B:4
- C:1/2
- D:1/4
答 案:B
解 析:因为是公比为2的数列,则,c=a*2^2,c/a=4,故选B
2、在 中,
中,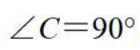 ,若
,若 ,则cosB的值为()
,则cosB的值为()
- A:1/2
- B:
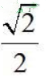
- C:

- D:1
答 案:B
多选题
1、已知函数y=1/2sin2x则()
- A:函数最大值为2
- B:函数最大值为1/2
- C:周期
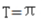
- D:周期
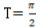
答 案:BC
解 析:A:sin2x最大值为1,则y=1/2sin2x的最大值为1/2,故A错B对。C:T=2π/W=2π/2=π,故C对D错
2、设{an}(n∈N*)是各项为正数的等比数列,q是其公比,Kn是其前n项的积,且K5K8,则下列选项中成立的是()
- A:0
- B:a7=1
- C:K9>K5
- D:K6与K7均为Kn的最大值
答 案:ABD
解 析:根据题意,依次分析选项:
对于B,若K6=K7,则a7=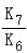 =1,故B正确;
=1,故B正确;
对于A,由K5<K6可得a6=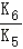 >1,则q=
>1,则q=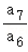 ∈(0,1),故A正确;
∈(0,1),故A正确;
对于C,由{an}是各项为正数的等比数列且q∈(0,1)可得数列单调递减,则有K9<K5,故C错误;
对于D,结合K5<K6,K6=K7>K8,可得D正确.
故选:ABD.
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
填空题
1、向量a=(m,4),b=(3,-2),且a∥b,则m=()
答 案:【﹣6】
解 析:向量a=(m,4),b=(3,-2),且a∥b可得12=-2m,解得m=-6故答案为:-6.
2、一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为______
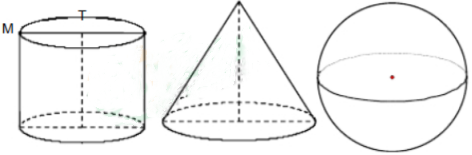
答 案:3:1:2



