2024年高职单招《数学》每日一练试题06月21日

2024年高职单招《数学》每日一练试题06月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、二项式（x+1）⁵的展开式共6项。（）  

答 案：对

解 析：n次方的展开式有n+1项，5次方的展开式有6项

2、函数f（x）=（x-1）（x²+3x-10）有3个零点。（）  

答 案：对

单选题

1、经过点P₁（4，9）、P₂（6，3）的直线的斜率为（）  

• A：1/3
• B：-1/3
• C：3
• D：-3

答 案：D

2、直线3x–5y+10=0在轴y上的截距为()  

• A：-2
• B：-10
• C：10
• D：2

答 案：D

解 析：如果通过直线方程求截距的斜率,那么把直线方程的形式写成点斜式。y=kx+b,那么k是直线的斜率,b是直线在y轴上的截距。本题中：3X-5Y+10=0写成：y=3/5x+2，所以k=3/5,b=2

多选题

1、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

2、已知向量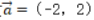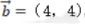，，则（）  

• A：
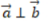
• B：
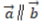
• C：
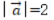
• D：

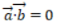
答 案：AD

解 析：若设a=(x1,y1)，b=(x2,y2)，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。本题中-2*4+2*4=0，则两个向量垂直

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、设集合A={0,a},B={-1,5,2},且A∩B={2},那么AUB=（）。

答 案：{-1,0,2,5}

解 析：因为A∩B={2},所以集合A中a=2,所以AUB={-1,0,2,5}.

2、若A、B为两独立事件，且________.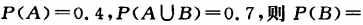

答 案：0.5

解 析：