2024年高职单招《数学》每日一练试题06月09日

2024年高职单招《数学》每日一练试题06月09日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、一个长方体，它的长、宽、高都扩大2倍，它的体积扩大6倍。()  

答 案：错

解 析：一个长方体，它的长、宽、高分别为1，1，1，体积为1。都扩大2倍，长宽高为2，2，2，体积为8。V原=abh；V扩=（2a）（2b）（2h）=8abh；所以体积是扩大了8倍

2、设π/4cosa。（）  

答 案：对

解 析：一全正，二正弦，三正切，四余弦（口诀）但是在第一象限以π/4发现为基准，当a大于π/4时，sina>cosa，当a小于π/4时，sinacosa，是正确的。

单选题

1、黄瑶拿一张正方形的纸按右图所示沿虚线连续对折后剪去带直角的部分，然后打开后的形状是()  

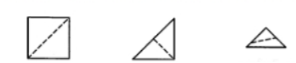
• A：
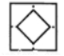
• B：
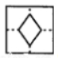
• C：
• D：

答 案：C

2、三角函数sin45°，cos16°，cos43°之间的大小关系是（　　）  

• A：cos43°＞cos16°＞sin45°
• B：cos16°＞cos43°＞sin45°
• C：cos16°＞sin45°＞cos43°
• D：cos43°＞sin45°＞cos16°

答 案：B

解 析：∵sin45°＝cos45°，又16°＜43°＜45°，余弦值随着角的增大而减小，∴cos16°＞cos43°＞sin45°。故选：B

多选题

1、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

2、已知等差数列{a_n}的前n项和为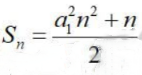，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
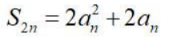
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、已知数据-3，-2，-1，1，2，a的中位数是-1，则a=_____  

答 案：-1

2、若函数y=(a²-3a+3)a^x(a>0且a≠1)是指数函数，则α=().

答 案：2

解 析：若函数y=(a²-3a+3)a^x是指数函数，则a²-3a+3=1,解得a=2或a=1(舍去).