2024年高职单招《数学》每日一练试题04月27日

2024年高职单招《数学》每日一练试题04月27日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、两直线2x-5y+6=0与5x+2y+5=0的位置关系是垂直。（）  

答 案：对

2、正多边形都是中心对称图形。（）  

答 案：错

解 析：当正多边形的边数为奇数时，该正多边形不是中心对称图形。

单选题

1、下列命题正确的是（）  

• A：对角线互相平分且相等的四边形是菱形
• B：三角形的内心到三角形三个顶点的距离相等
• C：过任意三点可以画一个圆
• D：对角线互相平分且有一个角是直角的四边形是矩形

答 案：D

解 析：A、对角线互相平分且相等的四边形是矩形，故该选项不符合题意；B、三角形的内心到三角形三个边的距离相等，故该选项不符合题意；C、不在同一直线上的三点确定一个圆，故该选项不符合题意；D、对角线互相平分且有一个角是直角的四边形是矩形，故该选项符合题意；故选：D

2、如图，在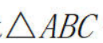中，，AC=3，AB=5，sinA的值为（）  

• A：4/5
• B：3/5
• C：3/4
• D：5/3

答 案：A

多选题

1、下列四个命题中正确的是（）  

• A：与圆有公共点的直线是该圆的切线
• B：垂直于圆的半径的直线是该圆的切线
• C：到圆心的距离等于半径的直线是该圆的切线
• D：过圆直径的端点，垂直于此直径的直线是该圆的切线

答 案：CD

解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。

2、设{a_n}(n∈N^*)是各项为正数的等比数列，q是其公比，K_n是其前n项的积，且K₅K₈，则下列选项中成立的是()  

• A：0
• B：a₇＝1
• C：K₉>K₅
• D：K₆与K₇均为K_n的最大值

答 案：ABD

解 析：根据题意，依次分析选项：
对于B，若K6＝K7，则a7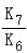＝＝1，故B正确；
对于A，由K5＜K6可得a6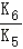＝＞1，则q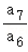＝∈（0，1），故A正确；
对于C，由{an}是各项为正数的等比数列且q∈（0，1）可得数列单调递减，则有K9＜K5，故C错误；
对于D，结合K5＜K6，K6＝K7＞K8，可得D正确．
故选：ABD．

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、从五名学生中选出四名参加数学、物理、生物、化学竞赛，其中甲不参加物理和化学竞赛，则不同的参赛方案的种类是_______.

答 案：72

解 析：分两类讨论

2、已知p:2x-6≥0,q:x≥a,若p是q的充分不必要条件，则实数a的取值范围是（）。

答 案：(-∞,3)

解 析：p:2x-6≥0,解得x≥3.q:x≥a,若p是q的充分不必要条件，则a<3.