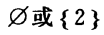2024年高职单招《数学》每日一练试题03月15日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、函数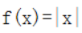 与
与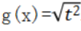 表示同一个函数。()
表示同一个函数。()
答 案:对
解 析:f(x)=|x|和g(x)=根号下 是同一函数.
是同一函数.
因为它们的定义域相同,都是R.
它们的对应规律相同,即自变量的绝对值等于函数值.
函数的两个要素均相同.
所以,它们是同一函数.
此外,它们的图象完全重合.
注意两点:
1.函数关系(特别提示:仅仅指函数关系)与表示自变量和函数的字母无关.
2.当我们比较两个函数关系异同的时候,往往是先化简,再比较.
如函数y=x/x与u=t0,分别化简为y=1,且x≠0;u=1,t≠0.按上述考察,它们是同一函数.
从形式上看,前者是分式函数,后者是幂函数.
“形式”是入门的向导,入门以后应抓住“本质”.
化简以后,也就是把它们的面纱揭去以后,原来它们是同一个函数.
最后,f(x)=|x|和g(x)=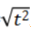 不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下
不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下 中是否含有x,不得而知.
中是否含有x,不得而知.
2、直线y=6平行于x轴。()
答 案:对
解 析:X轴是直线y=0,y等于任意非零数都与它平行。
单选题
1、下列命题中,正确的命题是()
- A:两条对角线相等的四边形是矩形
- B:两条对角线互相垂直且相等的四边形是正方形
- C:两条对角线相互垂直的四边形是菱形
- D:两条对角线互相平分的四边形是平行四边形
答 案:D
解 析:两条对角线互相平分且相等的四边形是矩形所以A错;正方形是特殊的矩形,具有矩形的所有特性,正方形的两条对角线相等且互相平分且垂直,所以B错;对角线互相垂直且平分的四边形为菱形或者对角线互相垂直的平行四边形为菱形,所以C错
2、已知函数f(x)=sin2x,则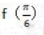 等于()
等于()
- A:1/2
- B:

- C:

- D:1
答 案:C
多选题
1、已知向量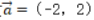 ,
,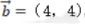 ,则()
,则()
答 案:AD
解 析:若设a=(x1,y1),b=(x2,y2),a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0。本题中-2*4+2*4=0,则两个向量垂直
2、设等差数列{an}的公差为d,其前n项和为Sn,且a1=-5,S3=-9,则()
- A:d=2
- B:S2,S4,S6为等差数列
- C:数列
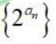 是等比数列
是等比数列 - D:S3是Sn的最小值
答 案:ACD
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1.
(2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1.
(3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
填空题
1、已知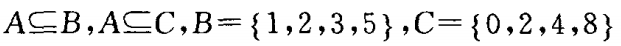 ,则A=_____。
,则A=_____。
答 案: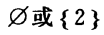
解 析:∵A⊆B,A⊆C,
∴A⊆(B∩C)
∵B={1,2,3,5},C={0,2,4,8},
∴B∩C={2}
而A⊆(B∩C)则A={2}或∅
先根据A⊆B,A⊆C可知A⊆(B∩C),然后求出B∩C,最后求出所求满足条件的A,最后得到结论.
2、若直线x+y+a=0(其中a为常数)经过圆x2+y2-2x+4y-6=0的圆心,则a的值是()
答 案: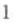
解 析:圆x2+y2-2x+4y-6=0的方程可化为(x-1)2+(y+2)2=11,所以圆心坐标为(1,—2).因为直线x+y+a=0过圆心,所以1-2+a=0,解得a=1.
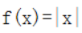 与
与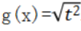 表示同一个函数。()
表示同一个函数。()  是同一函数.
是同一函数.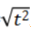 不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下
不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下 中是否含有x,不得而知.
中是否含有x,不得而知.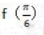 等于()
等于()


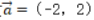 ,
,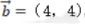 ,则()
,则()
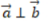
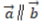
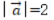
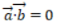
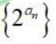 是等比数列
是等比数列
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合. 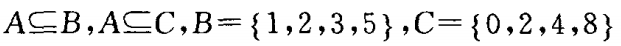 ,则A=_____。
,则A=_____。