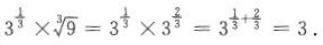2024年高职单招《数学》每日一练试题03月12日

2024年高职单招《数学》每日一练试题03月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、一个长方体，它的长、宽、高都扩大3倍，它的体积就扩大9倍。（）  

答 案：错

解 析：3×3×3＝27， 所以，如果把一个长方体的长、宽、高都同时扩大3倍，那么它的体积就扩大27倍。故答案为错误。  

2、若cosθ＞0，则θ是第一象限角。（）  

答 案：错

解 析：当sinθ＞0时，则θ是第一象限角，第一象限cosθ＞0，sinθ＞0；当sinθ＜0时，则θ是第四象限角，第四象限cosθ＞0，sinθ＜0

单选题

1、当5个整数从小到大排列，则中位数是4，如果这5个数的唯一众数是6，则这5个整数可能的最大和是()  

• A：21
• B：22
• C：23
• D：24

答 案：A

解 析：6是唯一的众数,因此必须至少出现二次,但由于是五个整数,并且4是中间数,按从小到大排序,因此可知4后排列的是两个6,而题目要最大的五整数和,可得出4之前两数分别是2,3,只有这亲才符合要求（如果4之前是负整数,五数和只可能越来越小；如果之前有1,仍然达到不到最大值）,得出最大的整数.因此最大整数和是21

2、一个箱子中有六个除了颜色之外完全一样的球，其中两个是红色，四个是黑色的，那么在里面随机拿出一个是红色的概率是多少（）  

• A：1/2
• B：1/3
• C：1/4
• D：1/6

答 案：B

解 析：六个球里两个是红色，则随机拿一个球，拿到红色的概率是2/6=1/3。故选B

多选题

1、已知向量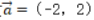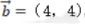，，则（）  

• A：
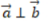
• B：
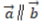
• C：
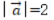
• D：

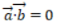
答 案：AD

解 析：若设a=(x1,y1)，b=(x2,y2)，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。本题中-2*4+2*4=0，则两个向量垂直

2、设{a_n}(n∈N^*)是各项为正数的等比数列，q是其公比，K_n是其前n项的积，且K₅K₈，则下列选项中成立的是()  

• A：0
• B：a₇＝1
• C：K₉>K₅
• D：K₆与K₇均为K_n的最大值

答 案：ABD

解 析：根据题意，依次分析选项：
对于B，若K6＝K7，则a7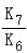＝＝1，故B正确；
对于A，由K5＜K6可得a6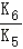＝＞1，则q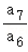＝∈（0，1），故A正确；
对于C，由{an}是各项为正数的等比数列且q∈（0，1）可得数列单调递减，则有K9＜K5，故C错误；
对于D，结合K5＜K6，K6＝K7＞K8，可得D正确．
故选：ABD．

主观题

1、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、焦点坐标为（-2,0）的抛物线的标准方程为__________  

答 案：y²=-8x

2、

答 案：3

解 析：