课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年高职单招《数学》每日一练试题08月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、-1与-4的等比中项是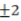 。()
。()
答 案:对
解 析:数列问题中的特殊性质,如果在等比数列a项和b项中,插入一个数G使a、G、b成等比数列,那么G叫做a、b的等比中项。如果G是a与b的等比中项,则有G/a=b/G。
2、“a=1”是“|a|=1”的充分但不必要条件。()
答 案:对
解 析:明显,当a=1时,a的绝对值=1,所以a=±1,不能推出a=1,所以是充分但不必要条件,故正确
单选题
1、 一个三位数除以53,商是a,余数是b(a,b都是正整数),则a+b的最大值是( )。
答 案:A
解 析:设三位数为x,若使a+b最大,则余数b肯定为52(0<b<53),有a=(x-52)÷53。此种情况下a最大为17,则a+b的最大值是17+52=69。
2、一天的时间共为86400秒,用科学记数法表示为()
- A:8.64×10^2秒
- B:86.4×10^3秒
- C:8.64×10^4秒
- D:0.8064×10^5秒
答 案:C
解 析:科学记数法是指把一个数表示成a×10的n次幂的形式,其中1≤a^2,故86400=8.64×10^4选C
多选题
1、已知等差数列{an}的前n项和为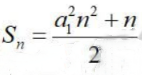 ,公差为d,则()
,公差为d,则()
- A:a1=1
- B:d=1
- C:2Sn-an=1+3+5+...+(2n-1)
- D:
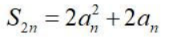
答 案:ABC
2、下列计算结果正确的是()
答 案:AC
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、已知两直线 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
答 案:(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时,l1与l2相交,即m≠0,m≠3且m≠-1.
(2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时,l1与l2平行,即m=0或m=-1.
(3)当-m(m-3)(m+1)=0且12-4m=0时,l1与l2重合,即m=3.
填空题
1、过点P(-2,0),且平行于向量v(0,3)的直线方程是________.
答 案:x=-2,如下图:
2、函数 在[-3,2]上的值域是().
在[-3,2]上的值域是().
答 案:[2,18]
解 析: ,当x=1时,函数f(x)有最小值2;当x=-3时,函数f(x)有最大值18.
,当x=1时,函数f(x)有最小值2;当x=-3时,函数f(x)有最大值18.
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
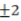 。()
。()
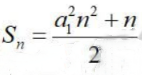 ,公差为d,则()
,公差为d,则()
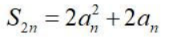

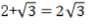
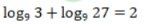
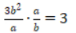

 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合. 
 在[-3,2]上的值域是().
在[-3,2]上的值域是(). ,当x=1时,函数f(x)有最小值2;当x=-3时,函数f(x)有最大值18.
,当x=1时,函数f(x)有最小值2;当x=-3时,函数f(x)有最大值18.


