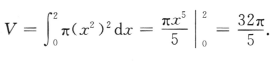2023年成考专升本《高等数学二》每日一练试题08月02日

2023年成考专升本《高等数学二》每日一练试题08月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、函数f(x)在[a，b]上连续是f(x)在该区间上可积的（）

• A：必要条件，但非充分条件
• B：充分条件，但非必要条件
• C：充分必要条件
• D：非充分条件，亦非必要条件

答 案：B

解 析：根据定积分的定义和性质，函数f(x)在[a，b]上连续，则f(x)在[a，b]上可积；反之，则不一定成立

2、设函数y＝cosx＋1，则dy＝（）.

• A：（sinx＋1）dx
• B：（cosx＋1）dx
• C：-sinxdx
• D：sinxdx

答 案：C

解 析：，故.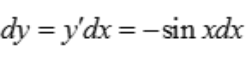

主观题

1、袋中有4张卡片，上面分别写有从1～4四个整数．让甲乙两人各自从中挑选一张，甲先挑选：选完后卡片不放回，同时再放入一张写有数字5的卡片，接下来让乙去挑选．记乙挑得的数字为X．试求随机变量X的概率分布，并求数学期望E(X)．

答 案：解：（1）随机变量X的可能取值为1，2，3，4，5．显然P(X＝1)＝P(X＝2)＝P(X＝3)＝P(X＝4)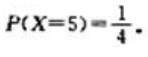，设事件A为甲挑到写有数字1的卡片，则．
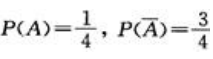事件B为乙挑到写有数字1的卡片，则P(B)＝P(X＝1)，因此
易知P(B|A)＝0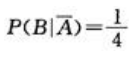，，因此．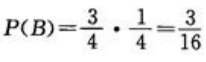
所以离散型随机变量X的概率分布为：
（2）．

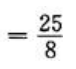2、设函数y＝f（x）是由方程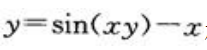确定的隐函数，求导数y′．

答 案：解：方程两边同时关于x求导得

填空题

1、（）．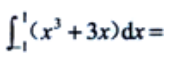

答 案：

解 析：因为积分区间关于原点对称，被积函数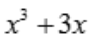为奇函数，故．

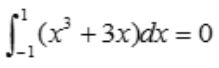2、两封信随机投入标号为1，2，3，4的四个邮筒，则1，2号邮筒各有一封信得概率为（）．

答 案：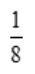

解 析：每封信有4种投法，共有4²种投法，1，2号邮筒各一封信的情况有2种，故其概率为．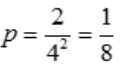

简答题

1、计算  

答 案：由洛必达法则有  

2、设D为由曲线y=x²，y=0，x=2所围成的图形. （1）求D的面积； （2）求D绕x轴旋转一周所得旋转体的体积.  

答 案：（1）D的面积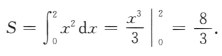 （2）D绕x轴旋转一周所得旋转体的体积