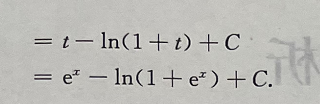2023年成考专升本《高等数学二》每日一练试题07月05日

2023年成考专升本《高等数学二》每日一练试题07月05日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、袋中有8个乒乓球，其中5个白色球，3个黄色球，从中一次任取2个乒乓球，则取出的2个球均为白色球的概率为（）.

• A：
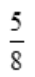
• B：
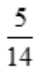
• C：
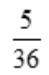
• D：

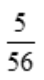
答 案：B

解 析：从袋中任意取2个球有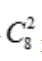种情况，取出的2个球均为白色球共有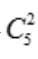种情况，则取出的2个球均为白色球的概率为.

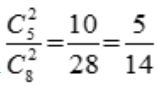2、已知函数f(x)的导函数f'(x)＝3x²－x－1，则曲线y＝f(x)在x＝2处切线的斜率是（）.

• A：3
• B：5
• C：9
• D：11

答 案：C

解 析：曲线y＝f(x)在x＝2处切线的斜率即为f(x)在x＝2时的导数值，即f‘’(2)=9.

3、事件A,B满足AB=A，则A与B的关系为（）

• A：A=B
• B：
• C：
• D：

答 案：B

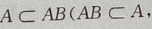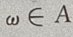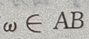解 析：AB=A，则按积的定义是当然的，即当时，必有，因而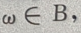

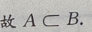
主观题

1、求一个正弦曲线与x轴所围成图形的面积（只计算一个周期的面积）．

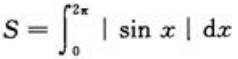
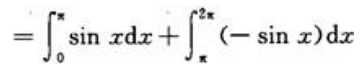
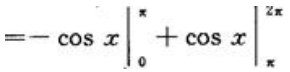
答 案：解：取从0～2π的正弦曲线如图，设所围图形面积为S，则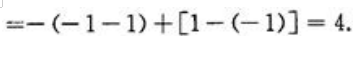注意到图形面积是对称的，可直接得出。

2、求函数f(x)＝x³－3x－2的单调区间和极值．

答 案：解：函数f(x)的定义域为（－∞，＋∞）．f'(x)＝3x²－3，令f'(x)＝0，得驻点x₁＝-1，x₂＝1．因此f(x)的单调增区间为（－∞，－1），（1，＋∞）；单调减区间为（－1，1）．f(x)的极大值为f(-1)＝0，极小值为f(1)＝－4．

3、求由方程siny＋xe^y＝0确定的曲线在点（0，π）处的切线方程．

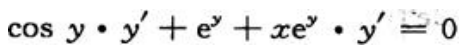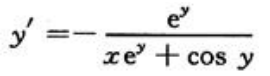答 案：解：方程两边对x求导得得所以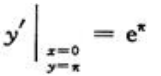,故所求切线方程为y－π＝e^π（x－0）,即e^πx－y＋π＝0

填空题

1、设函数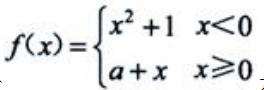在x＝0处连续，则a＝（）．

答 案：1

解 析：函数在x＝0处连续，则有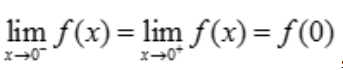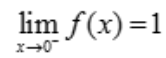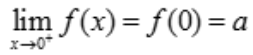，，，故a＝1．

2、若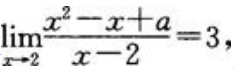则a＝（）．

答 案：－2

解 析：极限存在，则分母中含有公因式(x－2)，将x＝2代入中得a＝－2．

3、已知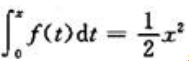，则＝()．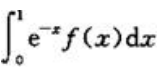

答 案：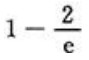

解 析：由题意可知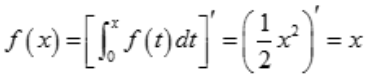，，故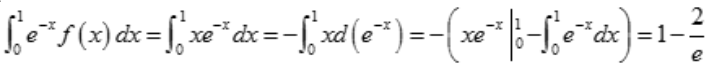

简答题

1、计算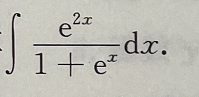

答 案：