2023年成考专升本《高等数学一》每日一练试题06月11日

2023年成考专升本《高等数学一》每日一练试题06月11日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、曲线y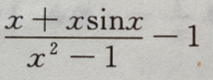的水平渐近线方程是（）

• A：y=2
• B：y=-2
• C：y=1
• D：y=-1

答 案：D

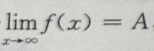解 析：所以水平渐近线为y=-1 ps：若，则y=A是水平渐近线，若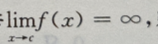则x=c是铅直渐近线。  

2、函数y＝f（x）在点x₀处可导的充分必要条件是（）。

• A：它在该点处的左导数和右导数存在
• B：它在该点处连续
• C：它在该点处存在极限
• D：它在该点处可微

答 案：D

解 析：D项，对于一元函数来说，函数在某一点可导和在某一点可微等价.A项，函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项，可导一定连续，但连续不一定可导，例如函数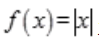在x=0连续但不可导；C项，极限存在与函数存在不存在必然联系。

3、在区间[－2，2]上，下列函数中不满足罗尔定理条件的是（）。

• A：
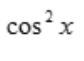
• B：
• C：
• D：1n（1＋x²）

答 案：B

解 析：A、C、D选项三个函数都是初等函数，且在[－2，2]上有定义，因此在区间[－2，2]上连续，且在区间两端点处函数值相等，又A选项的导函数为－2cosxsinx，C选项的导函数为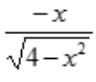，D选项的导函数为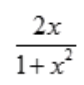，都在（－2，2）内有意义，所以A、C、D选项在（－2，2）内都可导，故它们都满足罗尔定理条件；而B选项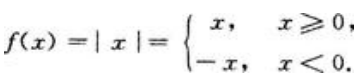，故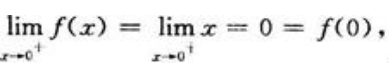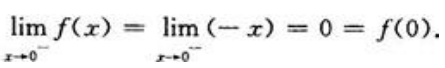则f（x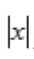）＝在x＝0连续，而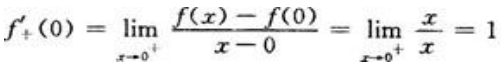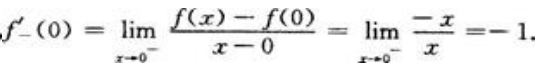，所以f（x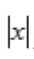）＝在x＝0处不可导，故f（x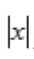）＝在（－2，2）内不可导，从而不满足罗尔定理使用条件。

主观题

1、设y＝（sinx）e^x＋2，求y'。

答 案：解：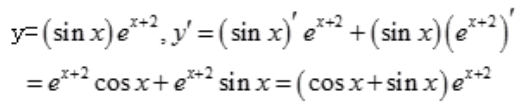

2、设切线l是曲线y＝x²＋3在点（1，4）处的切线，求由该曲线，切线，及y轴围成的平面图形的面积S。

答 案：解：y＝x²＋3，＝2x。切点（1，4），y'（1）＝2．故切线l的方程为y－4＝2（x－1）,即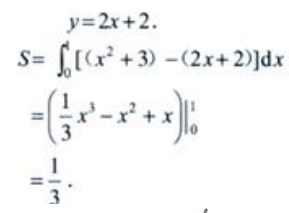

3、求曲线y＝x²、直线y＝2－x与x轴所围成的图形的面积A及该图形绕y轴旋转所得旋转体的体积V_y。

答 案：解：所围图形见下图。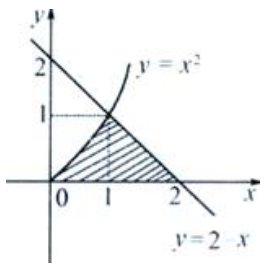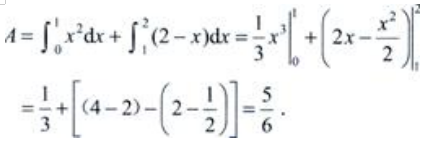A可另求如下：由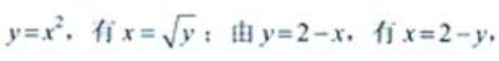故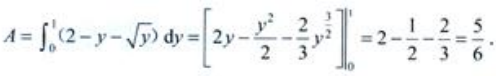

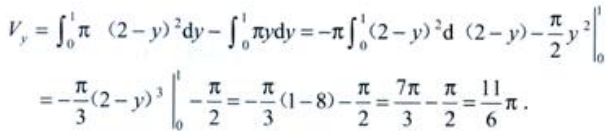
填空题

1、设函数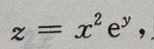则全微分dz=（）

答 案：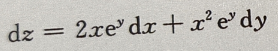

解 析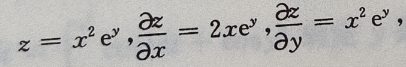：则

2、设函数y＝xⁿ，则y^（n＋1）＝（）。

答 案：

解 析：y＝xⁿ，则，。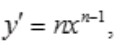

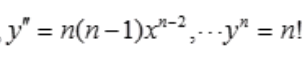3、级数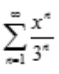的收敛区间是（）。

答 案：（-3,3）

解 析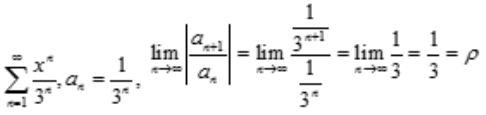：，因此收敛半径R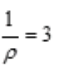＝，收敛区间为（－3,3）。

简答题

1、证明：当x>0时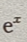>1+x.  

答 案：