2023年成考专升本《高等数学二》每日一练试题05月18日
2023-05-18 10:48:26 来源:吉格考试网
2023年成考专升本《高等数学二》每日一练试题05月18日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、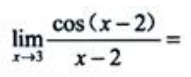 ().
().
- A:1
- B:cos1
- C:0
- D:
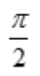
答 案:B
解 析:因为函数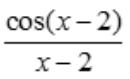 在x=3处连续,故
在x=3处连续,故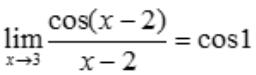 .
.
2、设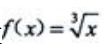 ,则
,则 ().
().
- A:
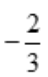
- B:
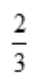
- C:1
- D:

答 案:A
解 析: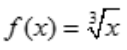 ,则
,则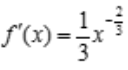 .
.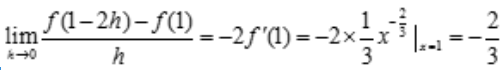 .
.
3、曲线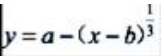 的拐点坐标为().
的拐点坐标为().
- A:(a,0)
- B:(a,-b)
- C:(a,b)
- D:(b,a)
答 案:D
解 析:函数的定义域为(-∞,+∞).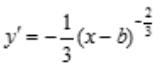 ,
,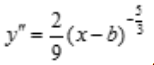 .当x=b,y=a时,y''不存在,因为f(x)在x=b连续,且当x<b时,y''<0,曲线y为凸;当x>b时,y''>0,曲线y为凹,故曲线的拐点为(b,a).
.当x=b,y=a时,y''不存在,因为f(x)在x=b连续,且当x<b时,y''<0,曲线y为凸;当x>b时,y''>0,曲线y为凹,故曲线的拐点为(b,a).
主观题
1、甲袋中有15只乒乓球,其中3只白球,7只红球,5只黄球,乙袋中有20只乒乓球,其中10只白球,6只红球,4只黄球.现从两袋中各取一只球,求两球颜色相同的概率.
答 案:解:样本空间的样本点应该是甲、乙两袋中的样本点之积,也就是从甲袋中取一个球再从乙袋中取一球的所有取法,即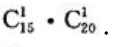 两球颜色相同的情况有三种,因此其样本点共有
两球颜色相同的情况有三种,因此其样本点共有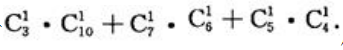 所以两球颜色相同的概率为
所以两球颜色相同的概率为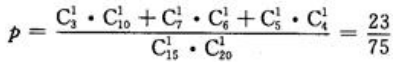
2、某射手击中10环的概率为0.26,击中9环的概率为0.32,击中8环的概率为0.36,求在一次射击中不低于8环的概率.
答 案:解:设A={击中10环),B={击中9环),C={击中8环),D={击中不低于8环),则D=A+B+C,由于A,B,C相互独立,所以P(D)=P(A+B+C)=P(A)+P(B)+P(C)=0.26+0.32+0.36=0.94
3、设函数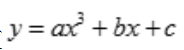 ,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
答 案:解: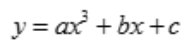 ,则
,则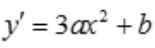 ,
,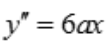 .由y(1)=-1,y(0)=1,y'(1)=0,得方程组
.由y(1)=-1,y(0)=1,y'(1)=0,得方程组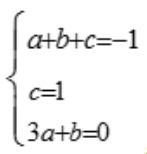 ,解得a=1,b=-3,c=1,所以
,解得a=1,b=-3,c=1,所以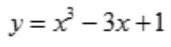 ,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线
,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线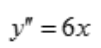 的凸区间为(-∞,0).
的凸区间为(-∞,0).
填空题
1、当x→∞时,函数数f(x)与 是等价无穷小量,则
是等价无穷小量,则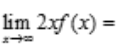 ().
().
答 案:2
解 析: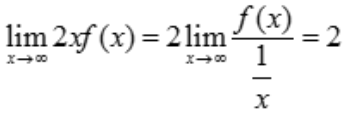 .
.
2、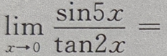 ()
()
答 案: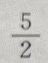
解 析: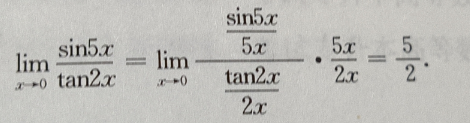
3、函数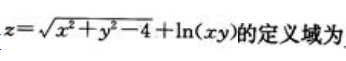 ()
()
答 案:
解 析:对于函数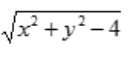 要求
要求 ,即
,即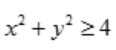 ;对于函数
;对于函数 要求xy>0,所以函数z的定义域为
要求xy>0,所以函数z的定义域为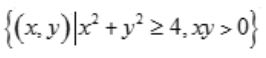 。
。
简答题
1、证明: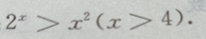
答 案:令 则
则 由于此式不便判定符号,故再求出
由于此式不便判定符号,故再求出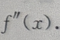 又因
又因
 所以f'(x)单调增加,故f'(x)>f'(4)=
所以f'(x)单调增加,故f'(x)>f'(4)= -8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加,故f(x)>f(4),即
-8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加,故f(x)>f(4),即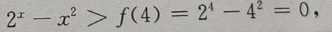 因此
因此



