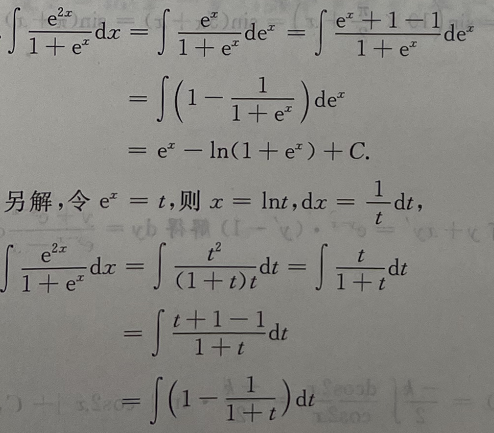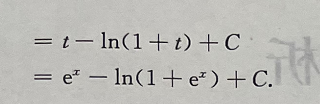2023年成考专升本《高等数学二》每日一练试题05月11日
2023-05-11 10:43:28 来源：吉格考试网
2023年成考专升本《高等数学二》每日一练试题05月11日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设函数z＝ex＋y2，则
（）.
- A：2y
- B：ex＋2y
- C：ex＋y2
- D：ex
答 案：D
解 析：当对x求导时，y相当于常量，故
，
.
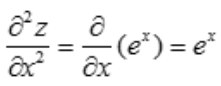2、设
则
＝（）.
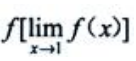- A：0
- B：-1
- C：-3
- D：-5
答 案：C
解 析：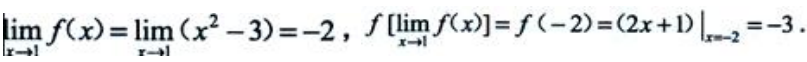
3、积分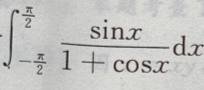
等于（）
- A：-1
- B：0
- C：1
- D：2
答 案：B
解 析：解法一，因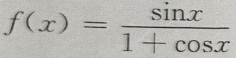
为奇函数，故由积分性质知，
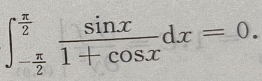解法二，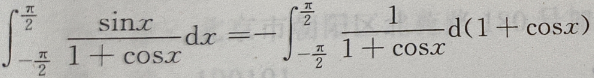
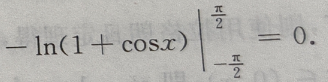
主观题
1、设函数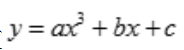
，在点x＝1处取得极小值-1，且点（0,1）是该曲线的拐点，试求常数a，b，c及该曲线的凹凸区间．
答 案：解：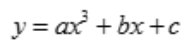
，则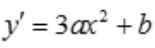
，
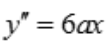．由y(1)＝－1，y(0)＝1，y'(1)=0，得方程组
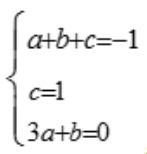，解得ａ＝１，ｂ＝－３，ｃ＝１，所以
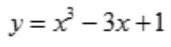，当ｘ＞０时，y''＞０，则曲线的凹区间为（０，＋∞）；当ｘ＜０时，y''＜０，则曲线
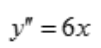的凸区间为（－∞，０）．
2、加工某零件需经两道工序，若每道工序的次品率分别为0.02与0.03，加工的工序互不影响，求此加工的零件是次品的概率．
答 案：解：A＝{第一道工序是次品)，B＝{第二道工序是次品)，C＝{产品是次品}，则C＝A＋B且Ａ与B相互独立，P(C)＝P(A＋B)＝P(A)＋P(B)－P(AB)＝P(A)＋P(B)－P(A)·P(B)＝0.02＋0.03－0.02×0.03＝0.0494．
3、己知离散型随机变量X的概率分布为
（1）求常数a；
（2）求X的数学期望EX．
答 案：解：（1）因为0.2＋0.1＋0.5＋a＝1，所以a＝0.2．（2）EX＝10×0.2＋20×0.1＋30×0.5＋40×0.2＝27．
填空题
1、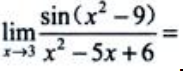
（）．
答 案：6
解 析：
2、已知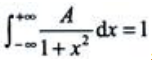
，则A＝()．
答 案：
解 析：
故A＝．
3、设函数z＝x2ey，则全微分dz＝（）．
答 案：2xeydx＋x2eydy
解 析：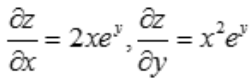
，故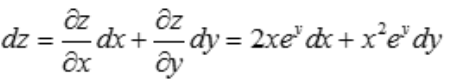
．
简答题
1、计算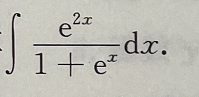
答 案：
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
