2023年成考专升本《高等数学二》每日一练试题05月08日

2023年成考专升本《高等数学二》每日一练试题05月08日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数f(x)在点x₀处有定义，是f(x)在点x0出连续的（）。  

• A：必要条件，但非充分条件
• B：充分条件，但非必要条件
• C：充分必要条件
• D：非充分条件，亦非必要条件

答 案：A

解 析：函数在f(x)在x₀处有定义不一定在该点连续，但是函数在x₀处连续在该点就一定有定义。

2、设函数f（x）=arctanx，则（）

• A：arctanx+C
• B： -arctanx +C
• C：
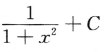
• D：

答 案：A

解 析：

3、广义积分（）

• A：
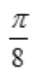
• B：
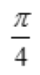
• C：
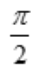
• D：π

答 案：Ｂ

解 析：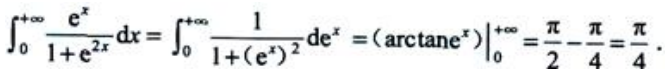

主观题

1、在半径为R的半圆内作一内接矩形，其中的一边在直径上，另外两个顶点在圆周上（如图所示）．当矩形的长和宽各为多少时矩形面积最大？最大值是多少？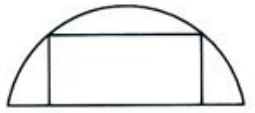

答 案：解：如图所示，设x轴通过半圆的直径，y轴垂直且平分直径．设OA＝x，则AB＝，矩形面积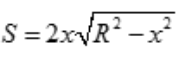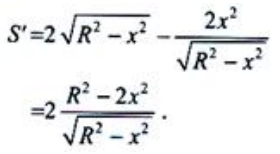．令s'=0，得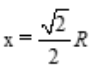（舍去负值）．
由于只有唯一驻点，根据实际问题x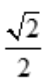＝，必为所求，则AB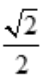＝R．所以，当矩形的长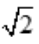为R、宽为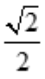R时，矩形面积最大，且最大值S＝R²．

2、袋中有10个乒乓球．其中6个白球、4个黄球，随机地抽取两次，每次取1个，不放回．设A＝{第一次取到白球），B＝{第二次取到白球}，求P（B|A）．

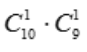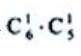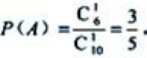答 案：解：因为样本空间的基本事件有个．而AB表示第一次取白球且第二次也取白球，故引起事件AB的基本事件有个，所以而；所以；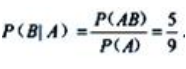

3、设函数y＝ln（x²＋1），求dy．

答 案：解：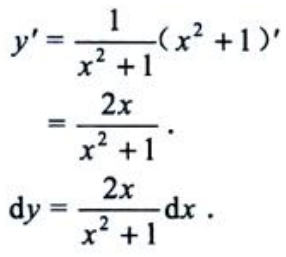

填空题

1、已知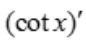＝f(x)，则()．

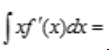答 案：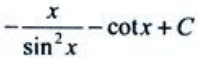

解 析：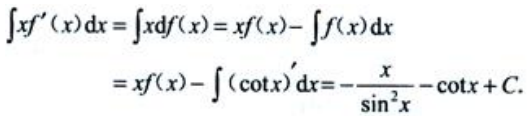

2、设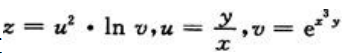，则dz＝（）

答 案：

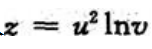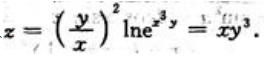解 析：方法一：把u，v代入中，有故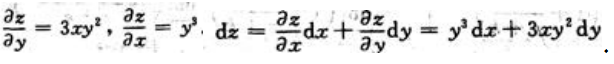方法二：按复合求导法则求导，再代入全微分公式中，。
所以
方法三：利用一阶微分形式的不变性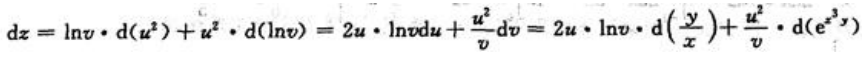

3、设z=x³y+xy³，则（）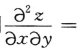  

答 案：3x²+3y²

解 析：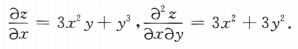

简答题

1、求由曲线y＝x²与x＝2，y＝0所围成图形分别绕x轴，y轴旋转一周所生成的旋转体体积．

答 案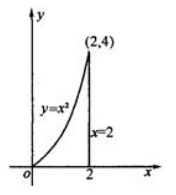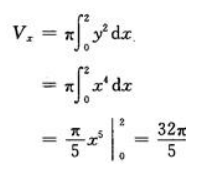： 绕y轴旋转一周所得的旋转体体积为