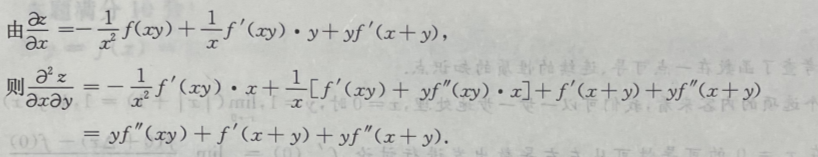课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年成考专升本《高等数学二》每日一练试题05月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设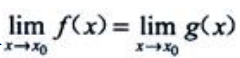 ,则
,则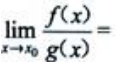 ().
().
答 案:D
解 析:做该题时若不假思索,很容易错选B为答案.但假若对极限的定义有正确理解,特别是能联想到如 的不定型,便知答案是D.事实上,
的不定型,便知答案是D.事实上,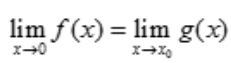 ,则可能有以下三种情况
,则可能有以下三种情况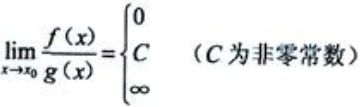
2、函数f(x)=1-x3在区间(-∞,+∞)().
- A:单调增加
- B:单调减少
- C:先单调增加,后单调减少
- D:先单调减少,后单调增加
答 案:B
解 析:对任意的x≠0,有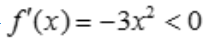 ,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少.
,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少.
3、下列命题正确的是().
- A:函数f(x)的导数不存在的点,一定不是f(x)的极值点
- B:若x0为函数f(x)的驻点,则x0必为f(x)的极值点
- C:若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
- D:若函数f(x)在点x0处连续,则f'(x0)一定存在
答 案:C
解 析:AD两项,设f(x)=|x|,显然x=0是函数的极小值点,且函数在该点也连续,但函数在该点不可导;B项,设f(x)=x3,显然x0=0是函数的驻点,但x0=0不是函数的极值点;C项,根据函数在点x0处取极值的必要条件的定理,可知选项C是正确的.
主观题
1、设函数z=z(x,y)是由方程 所确定的隐函数,求出dz.
所确定的隐函数,求出dz.
答 案:解:设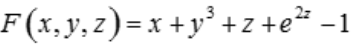 .由于
.由于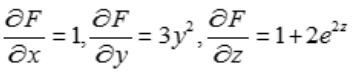 ,得
,得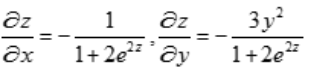 ,所以
,所以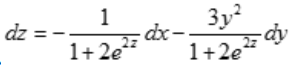 .
.
2、设f(x)是(-∞,+∞)内连续的偶函数,证明: .
.
答 案:证:设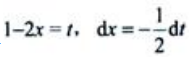 ,当x=0时t=1,x=1时t=1.所以
,当x=0时t=1,x=1时t=1.所以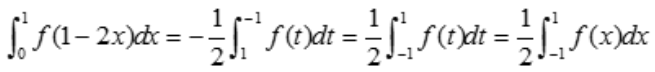 又f(x)是(-∞,+∞)内连续的偶函数,故
又f(x)是(-∞,+∞)内连续的偶函数,故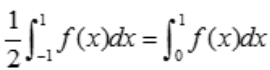 ,即
,即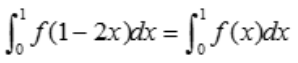 .
.
3、计算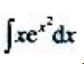 .
.
答 案:解: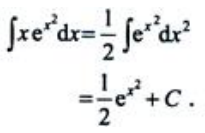
填空题
1、若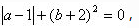 则
则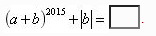
答 案:1
2、曲线y=x5-10x2+8的拐点坐标(x0,y0)=().
答 案:(1,-1)
解 析: ,令y''=0,得x=1,y=-1.当x<1时,y''<0;当x>1时,y''>0.故(1,-1)为曲线的拐点.
,令y''=0,得x=1,y=-1.当x<1时,y''<0;当x>1时,y''>0.故(1,-1)为曲线的拐点.
3、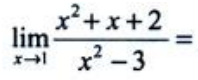 ().
().
答 案:-2
解 析: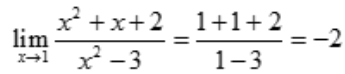 .
.
简答题
1、设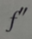 存在,
存在,
答 案: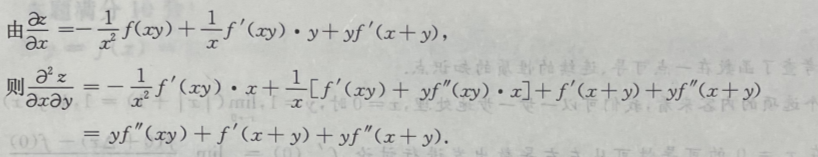
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
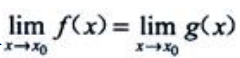 ,则
,则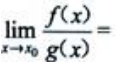 ().
(). 的不定型,便知答案是D.事实上,
的不定型,便知答案是D.事实上,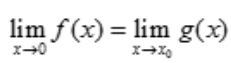 ,则可能有以下三种情况
,则可能有以下三种情况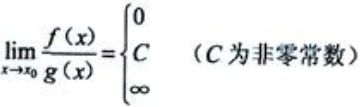
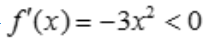 ,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少.
,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少. 所确定的隐函数,求出dz.
所确定的隐函数,求出dz.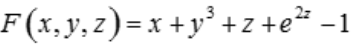 .由于
.由于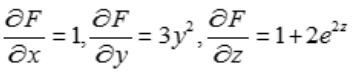 ,得
,得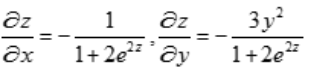 ,所以
,所以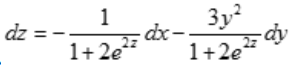 .
. .
.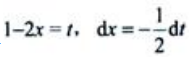 ,当x=0时t=1,x=1时t=1.所以
,当x=0时t=1,x=1时t=1.所以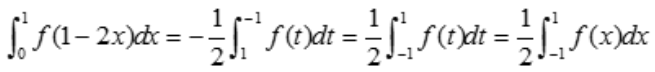 又f(x)是(-∞,+∞)内连续的偶函数,故
又f(x)是(-∞,+∞)内连续的偶函数,故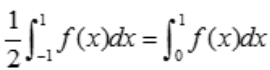 ,即
,即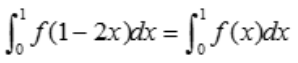 .
.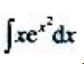 .
.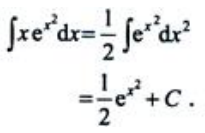
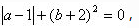 则
则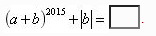
 ,令y''=0,得x=1,y=-1.当x<1时,y''<0;当x>1时,y''>0.故(1,-1)为曲线的拐点.
,令y''=0,得x=1,y=-1.当x<1时,y''<0;当x>1时,y''>0.故(1,-1)为曲线的拐点.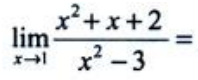 ().
().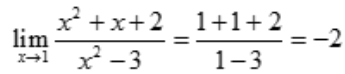 .
.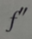 存在,
存在,