2023年成考专升本《高等数学二》每日一练试题04月06日
2023-04-06 10:56:59 来源：吉格考试网
2023年成考专升本《高等数学二》每日一练试题04月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、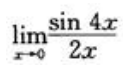
等于（）.
- A：0
- B：
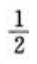
- C：2
- D：1
答 案：C
解 析：
.
2、设函数f(x)＝cos2x，则f'(x)＝（）.
- A：2sin2x
- B：－2sin2x
- C：sin2x
- D：－sin2x
答 案：B
解 析：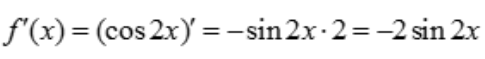
.
3、设ｚ＝ｚ(ｘ，ｙ)是由方程yz＋x＝１确定的函数，则
等于（）.
- A：
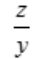
- B：
- C：－
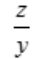
- D：－
答 案：C
解 析：方程两边对y求导，
.
主观题
1、己知某篮球运动员每次投篮投中的概率是0.9，记X为他两次独立投篮投中的次数．（1）求X的概率分布；
（2）求X的数学期望EX．
答 案：解：（1）X可能的取值为0，1，2；
因此X的概率分布为 
（2）数学期望
EX＝0×0.1＋1×0.18＋2×0.81＝1.80
2、在1、2、3、4、5、6的六个数字中，一次取两个数字，试求取出的两个数字之和为6的概率．
答 案：解：设A＝{两个数字之和为6）．基本事件数为：六个数字中任取两个数字的取法共有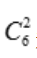
种，取出的两个数字之和为6只有2种情况，即取出的是1与5和2与4，所以
3、函数z＝f(x，y)由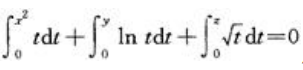
所确定，求
．
答 案：解：方程两边关于x求偏导数，得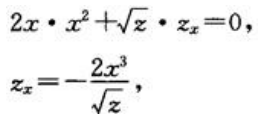
即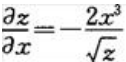
．方程两边关于y求偏导数，得
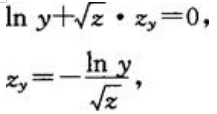即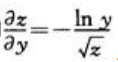
．
填空题
1、若f（x）在x＝a处可导，则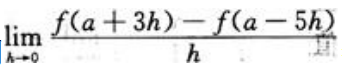
＝（）．
答 案：8f'(a)
解 析：因为f（x）在x＝a处可导，
2、设函数z＝ex＋y，则dz＝（）．
答 案：exdx＋dy
解 析：
，故
。
3、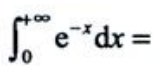
（）．
答 案：1
解 析：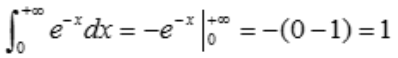
．
简答题
1、求函数
的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.
答 案：
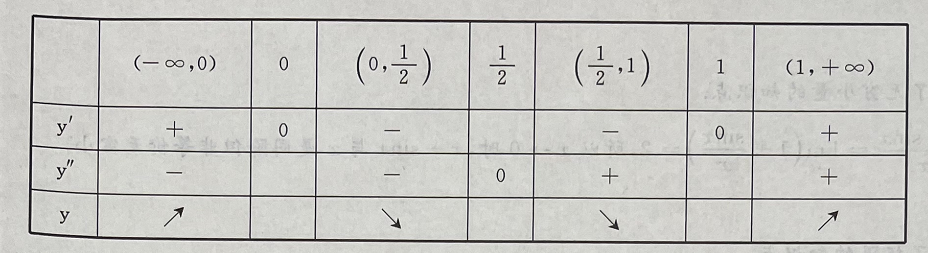所以函数y的单调增区间为
单调减区间为（0,1）；函数y的凸区间为
凹区间为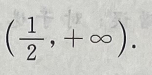
故x=0时，函数有极大值0，x=1时，函数有极小值-1，且点
为拐点，因
不存在，且
没有无意义的点，故函数没有渐近线。
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
