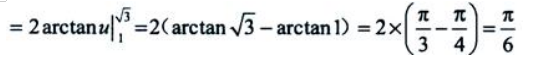2023年成考专升本《高等数学二》每日一练试题03月21日
2023-03-21 10:45:47 来源:吉格考试网
2023年成考专升本《高等数学二》每日一练试题03月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知P(A)= ,P(B)=
,P(B)= ,下列结论正确的是().
,下列结论正确的是().
- A:P(AB)=
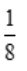
- B:若A,B互斥,则P(AB)=
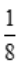
- C:若A,B独立,则P(AB)=
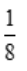
- D:若A,B对立,则P(AB)=

答 案:C
解 析:互斥,则P(AB)=0,P(A+B)=P(A)+P(B);A,B独立,则P(AB)=P(A)×P(B);A,B对立,则P(A)+P(B)=1.
2、曲线y=1-x2与x轴所围成的平面图形的面积S=().
- A:2
- B:
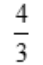
- C:1
- D:

答 案:B
解 析:y=1-x2与x轴的交点为(1,0),(1,0).则面积为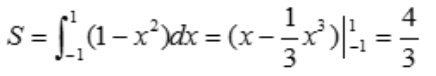
3、在下列函数中,当x→0时,函数f(x)的极限存在的是().
- A:
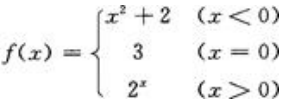
- B:
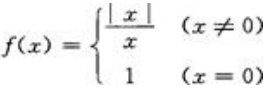
- C:
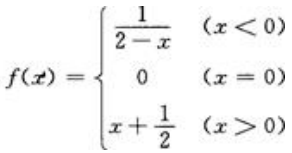
- D:
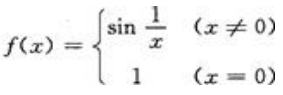
答 案:C
解 析:A项,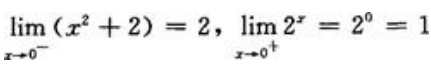 ,所以当x→0时极限不存在;B项,
,所以当x→0时极限不存在;B项,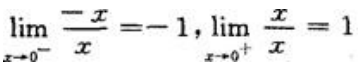 ,所以当x→0时极限不存在;C项,
,所以当x→0时极限不存在;C项,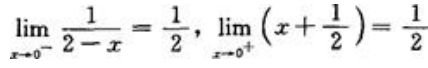 ,所以当x→0时极限存在;D项,
,所以当x→0时极限存在;D项,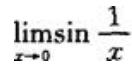 ,极限不存在.
,极限不存在.
主观题
1、袋中有4张卡片,上面分别写有从1~4四个整数.让甲乙两人各自从中挑选一张,甲先挑选:选完后卡片不放回,同时再放入一张写有数字5的卡片,接下来让乙去挑选.记乙挑得的数字为X.试求随机变量X的概率分布,并求数学期望E(X).
答 案:解:(1)随机变量X的可能取值为1,2,3,4,5.显然P(X=1)=P(X=2)=P(X=3)=P(X=4),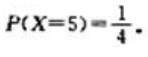 设事件A为甲挑到写有数字1的卡片,则
设事件A为甲挑到写有数字1的卡片,则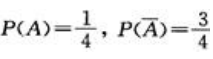 .
.
事件B为乙挑到写有数字1的卡片,则P(B)=P(X=1),因此
易知P(B|A)=0,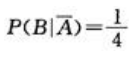 ,因此
,因此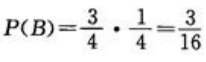 .
.
所以离散型随机变量X的概率分布为:
(2)
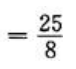 .
.
2、设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面图形(如图所示).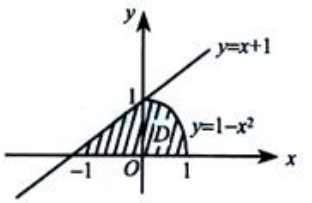 (1)求平面图形D的面积S;
(1)求平面图形D的面积S;
(2)求平面图形D绕x轴旋转一周所成旋转体的体积Vx.
答 案:解:(1)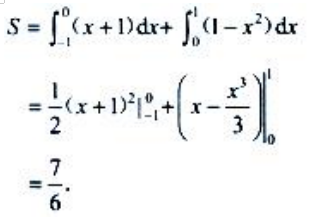 (2)
(2)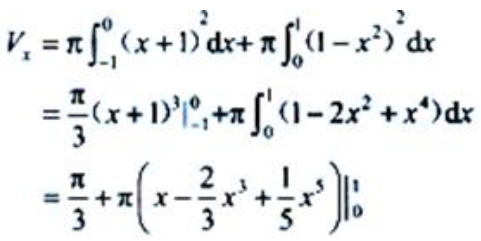
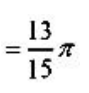
3、求函数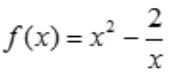 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
答 案:解:f(x)的定义域为(-∞,0)∪(0,+∞),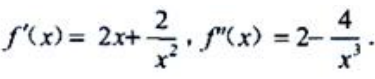 令
令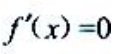 ,得x=-1.令
,得x=-1.令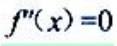 ,得
,得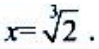
列表得
所以函数f(x)的单调减少区间为(-∞,-1),单调增加区间(-1,0),(0,+∞);
f(-1)=3为极小值,无极大值.
函数f(x)的凹区间为(-∞,0),(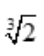 ,+∞),凸区间为(0,
,+∞),凸区间为(0,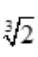 ),拐点坐标为(
),拐点坐标为(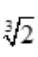 ,0).
,0).
填空题
1、 =().
=().
答 案: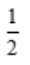
解 析: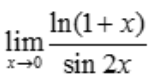 =
=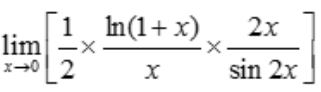 =
=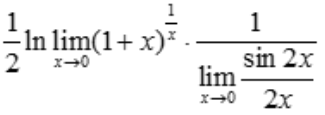 =
=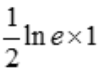 =
=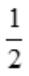 .
.
2、若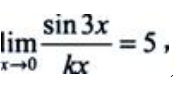 则k=().
则k=().
答 案: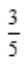
解 析: ,
,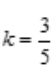 .
.
3、设y=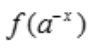 ,且f可导,则y'=().
,且f可导,则y'=().
答 案: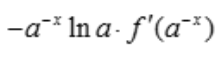
解 析: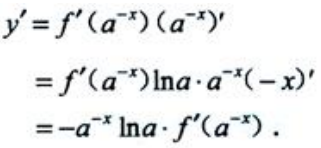
简答题
1、计算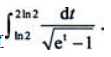
答 案: 设
设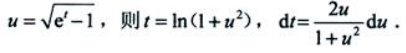 则
则