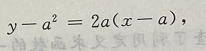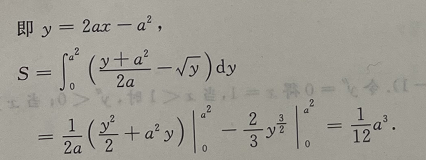2023年成考专升本《高等数学二》每日一练试题02月18日

2023年成考专升本《高等数学二》每日一练试题02月18日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

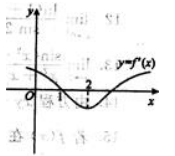
1、根据f(x)的导函数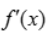的图像（如图所示），判断下列结论正确的是（ ）．

• A：在（∞，1）上f(x)是单调递减的
• B：在（∞，2）上f(x)是单调递减的
• C：f(1)为极大值
• D：f(1)为极小值

答 案：C

解 析：在x轴上方的曲线是表示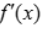>0,而x轴下方的曲线则表示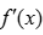<0,注在x＝1处的左边即x<1时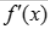>0,而2>x>1时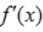<0，根据极值的第一充分条件可知f(1)为极大值．  

2、用A表示事件“甲考核通过且乙考核不通过”，则其对立事件为（）.

• A：“甲考核不通过，乙考核通过”
• B：“甲、乙考核都通过”
• C：“甲考核不通过”
• D：“甲考核不通过或乙考核通过”

答 案：D

解 析：A表示事件“甲考核通过且乙考核不通过”，令M事件为“甲考核通过”，N事件为“乙考核不通过”，则A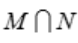＝，则其对立事件就应该是M事件不发生或N不发生.

3、已知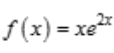，则f'(x)＝（）.

• A：
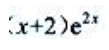
• B：
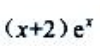
• C：
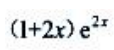
• D：

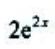
答 案：C

解 析：.

主观题

1、盒中装着标有数字1、2、3、4的乒乓球各2个，从盒中任意取出3个球，求下列事件的概率：（1）A＝{取出的3个球上最大的数字是4}．
（2）B＝{取出的3个球上的数字互不相同}．

答 案：解：基本事件任意取出3个球共有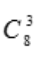种．（1）取出的3个球上最大的数字是4，有两种可能，即从中取出一个数字为4的球或取出两个数字为4的球，取出一个数字为4的球有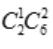种，取出两个数字为4的球有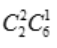种．事件A中的基本事件为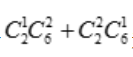种．所以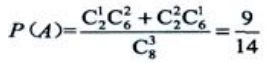（2）事件B中的基本事件数的计算可以分两步进行：
先从1，2，3，4的4个数中取出3个数的方法为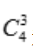种．
由于每1个数有2个球，再从取出的3个不同数字的球中各取1个球，共有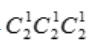种．
根据乘法原理可知取出的3个球上的数字互不相同的取法共有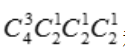种．
所以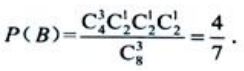

2、求．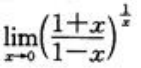

答 案：解：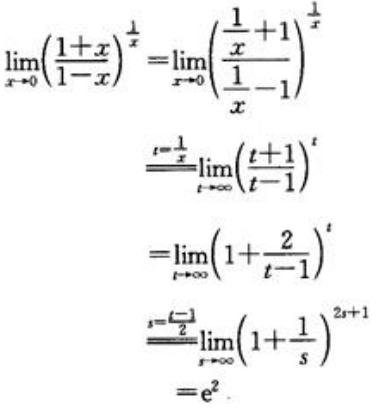

3、若，求a与b．

答 案：解：若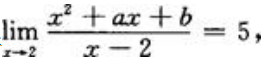则当x→2时，x²＋ax＋b与x－2为同阶无穷小量，令x²＋ax＋b＝(x－2)(x＋k)①则＝5，此时k＝3，代入①式得x²＋ax＋b＝(x－2)(x＋3)，
即x²＋ax＋b＝x²＋x－6，
所以a＝1，b＝-6．

填空题

1、已知f（x）的一个原函数为2lnx,则()．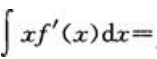

答 案：

解 析：由分部积分法可知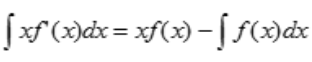，由题可知f（x）的一个原函数为2lnx，所以，故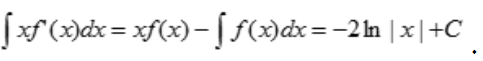

2、曲线y＝x³＋3x²＋1的拐点坐标为（）．

答 案：（－1，3）

解 析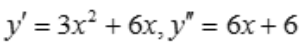：，令y''=0，得x=-1，y=3.当x＜-1时y''＜0；当x＞-1时y''＞0.故曲线的拐点为（－1，3）．

3、设函数z＝x²e^y，则全微分dz＝（）．

答 案：2xe^ydx＋x²e^ydy

解 析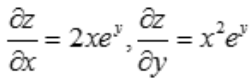：，故．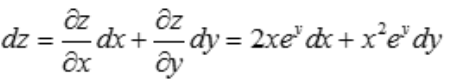

简答题

1、求曲线y=x²与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.

答 案：如图所示，在x=a出切线的斜率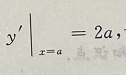为切线方程为