2023年成考专升本《高等数学一》每日一练试题02月12日
2023-02-12 10:42:31 来源:吉格考试网
2023年成考专升本《高等数学一》每日一练试题02月12日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设z=2x2+3xy-y2,则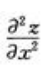 等于()。
等于()。
- A:4
- B:3
- C:2
- D:-2
答 案:A
解 析: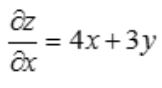 ,
,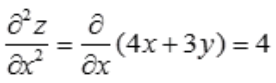 。
。
2、设z=3x2+5y,则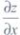 =()。
=()。
- A:5y
- B:3x
- C:6x
- D:6x+5
答 案:C
解 析:z=3x2+5y, 。
。
3、设函数y=f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),曲线f(x)在(a,b)内平行于x轴的切线()。
- A:仅有一条
- B:至少有一条
- C:不存在
- D:不一定存在
答 案:B
解 析:由罗尔定理可知,至少存在一个 ,使得
,使得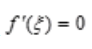 .而
.而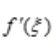 表示函数在
表示函数在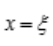 处的切线的斜率,所以曲线f(x)在(a,b)内平行于x轴的切线至少有一条。
处的切线的斜率,所以曲线f(x)在(a,b)内平行于x轴的切线至少有一条。
主观题
1、计算二重积分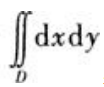 ,其中D是由曲线y=1-x2与y=x2-1所围成.
,其中D是由曲线y=1-x2与y=x2-1所围成.
答 案:解:积分区域D如图所示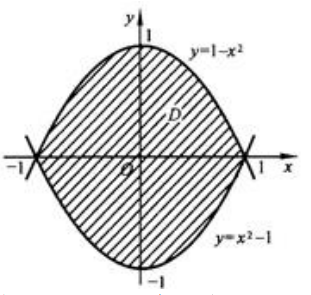 。
。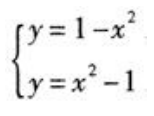 解得两组解,对应两个交点(-1,0),(1,0)。
解得两组解,对应两个交点(-1,0),(1,0)。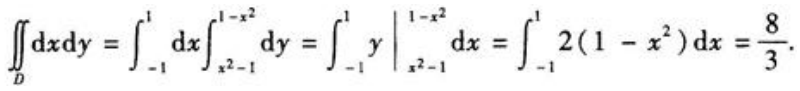
2、已知f(π)=1,且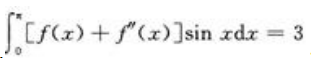 ,求f(0)。
,求f(0)。
答 案:解:
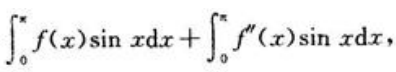 对
对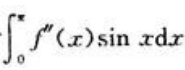 采用凑微分和分部积分后与
采用凑微分和分部积分后与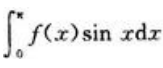 相加,代入条件即可求出f(0)。因为
相加,代入条件即可求出f(0)。因为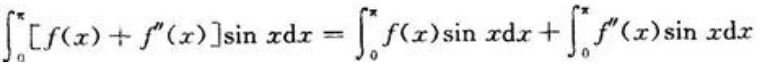
而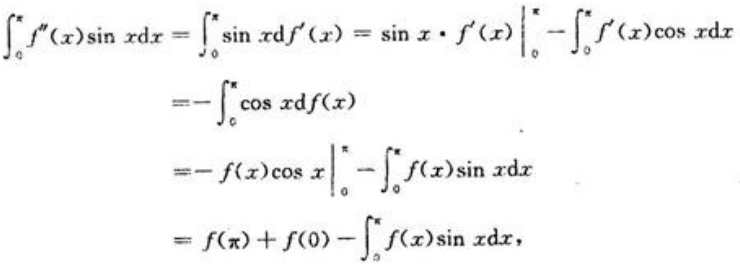
所以
又f(π)=1,所以f(0)=2。
3、判定级数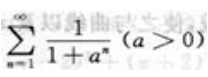 的敛散性.
的敛散性.
答 案:解: 含有参数a>0,要分情况讨论:(1)如果0<a<1,则
含有参数a>0,要分情况讨论:(1)如果0<a<1,则 ,由级数收敛的必要条件可知,原级数发散。(2)如果a>1,令
,由级数收敛的必要条件可知,原级数发散。(2)如果a>1,令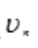 =
=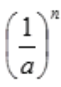 ;因为
;因为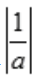 <1,因而
<1,因而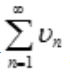 是收敛的,比较法:
是收敛的,比较法: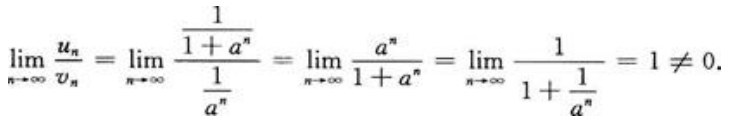
所以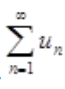 也收敛。
也收敛。
(3)如果a=1,则 所以
所以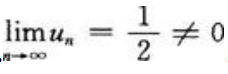 ,由级数收敛的必要条件可知,原级数发散。所以
,由级数收敛的必要条件可知,原级数发散。所以
填空题
1、若积分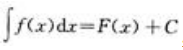 ,则积分
,则积分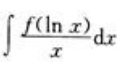 =()。
=()。
答 案:F(1nx)+C
解 析: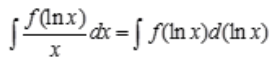 ,因为
,因为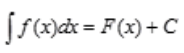 ,所以令
,所以令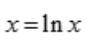 得
得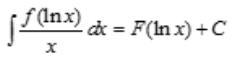 。
。
2、曲线y=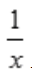 与直线y=x,x=2围成的图形面积为()。
与直线y=x,x=2围成的图形面积为()。
答 案: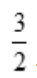 -1n2
-1n2
解 析:由题作图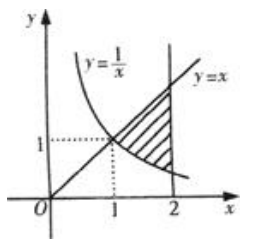 ,由图可知所求面积为
,由图可知所求面积为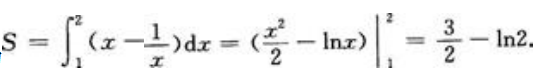
3、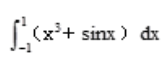 =()。
=()。
答 案:
解 析:被积函数x3+sinx为奇函数,且积分区域关于原点对称,由定积分的对称性得 =0。
=0。
简答题
1、讨论级数 的敛散性.
的敛散性.
答 案:因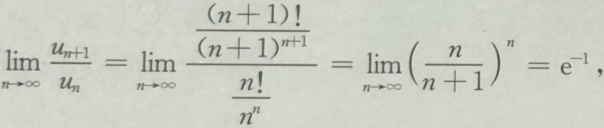 所以级数收敛.
所以级数收敛.



